Exam 9: Systems of Equations and Inequalities
Exam 1: Fundamental Concepts of Algebra150 Questions
Exam 2: Equations and Inequalities142 Questions
Exam 3: Functions and Graphs147 Questions
Exam 4: Polynomial and Rational Functions147 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions144 Questions
Exam 6: The Trigonometric Functions150 Questions
Exam 7: Analytic Trigonometry150 Questions
Exam 8: Applications of Trigonometry144 Questions
Exam 9: Systems of Equations and Inequalities147 Questions
Exam 10: Sequences, Series and Probability150 Questions
Exam 11: Topics From Analytic Geometry150 Questions
Select questions type
Three average monthly low temperatures for Detroit are listed in the table. 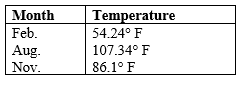 Let
Let 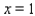 correspond to January,
correspond to January, 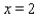 to February, . . . , and
to February, . . . , and 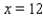 to December. Determine a quadratic function
to December. Determine a quadratic function 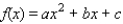 that interpolates the data - that is, determine the constants a, b, and c such that
that interpolates the data - that is, determine the constants a, b, and c such that 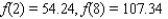 , and
, and 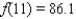 .
.
(Multiple Choice)
4.8/5  (34)
(34)
A manufacturer of tennis rackets makes a profit of $15 on each oversized racket and $10 on each standard racket. To meet dealer demand, daily production of standard rackets should be between 25 and 75, and production of oversized rackets should be between 8 and 27. To maintain high quality, the total number of rackets produced should not exceed 75 per day. How many of each type should be manufactured daily to maximize the profit?
(Multiple Choice)
4.8/5  (28)
(28)
A stationary company makes two types of notebooks: a deluxe notebook with subject dividers, which sells for $1.1, and a regular notebook, which sells for $0.85. The production cost is $1.00 for each deluxe notebook and $0.75 for each regular notebook. The company has the facilities to manufacture between 2,000 and 3,000 deluxe and between 3,000 and 6,000 regular notebooks, but not more than 7,000 altogether. How many notebooks of each type should be manufactured to maximize the difference between the selling prices and the production cost?
(Multiple Choice)
5.0/5  (32)
(32)
A small firm manufactures bookshelves and desks for microcomputers. For each product it is necessary to use a table saw and a power router. To manufacture each bookshelf, the saw must be used for 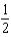 hour and the router for 1 hour. A desk requires the use of each machine for 2 hours. The profits are $20 per bookshelf and $50 per desk. If the saw can be used for 8 hours per day and the router for 12 hours per day, how many bookshelves and desks should be manufactured each day to maximize the profit?
hour and the router for 1 hour. A desk requires the use of each machine for 2 hours. The profits are $20 per bookshelf and $50 per desk. If the saw can be used for 8 hours per day and the router for 12 hours per day, how many bookshelves and desks should be manufactured each day to maximize the profit?
(Multiple Choice)
4.9/5  (40)
(40)
Find the maximum and minimum values of the objective function 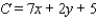 on the region in the figure.
on the region in the figure. 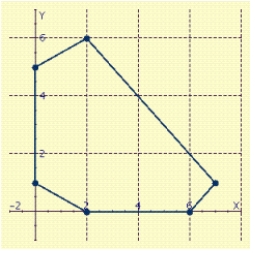
(Multiple Choice)
4.9/5  (35)
(35)
A manufacturer of tennis rackets makes a profit of $14 on each oversized racket and $8 on each standard racket. To meet dealer demand, daily production of standard rackets should be between 25 and 77, and production of oversized rackets should be between 10 and 30. To maintain high quality, the total number of rackets produced should not exceed 77 per day. How many of each type should be manufactured daily to maximize the profit?
(Multiple Choice)
4.8/5  (39)
(39)
Showing 61 - 80 of 147
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)