Exam 9: Systems of Equations and Inequalities
Exam 1: Fundamental Concepts of Algebra150 Questions
Exam 2: Equations and Inequalities142 Questions
Exam 3: Functions and Graphs147 Questions
Exam 4: Polynomial and Rational Functions147 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions144 Questions
Exam 6: The Trigonometric Functions150 Questions
Exam 7: Analytic Trigonometry150 Questions
Exam 8: Applications of Trigonometry144 Questions
Exam 9: Systems of Equations and Inequalities147 Questions
Exam 10: Sequences, Series and Probability150 Questions
Exam 11: Topics From Analytic Geometry150 Questions
Select questions type
Three average monthly low temperatures for Detroit are listed in the table.  Let
Let 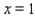 correspond to January,
correspond to January, 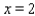 to February, . . . , and
to February, . . . , and 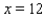 to December. Determine a quadratic function
to December. Determine a quadratic function 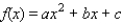 that interpolates the data - that is, determine the constants a, b, and c such that
that interpolates the data - that is, determine the constants a, b, and c such that 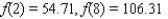 , and
, and 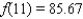 .
.
(Multiple Choice)
4.8/5  (34)
(34)
Let 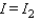 be the identity matrix of order 2, and let
be the identity matrix of order 2, and let 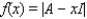 . Find the polynomial
. Find the polynomial 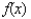 for the given matrix A in order to find the zeros of
for the given matrix A in order to find the zeros of 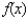 .
(In the study of matrices,
.
(In the study of matrices, 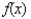 is the characteristic polynomial of A, and the zeros of
is the characteristic polynomial of A, and the zeros of 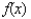 are the characteristic values (eigenvalues) of A.)
are the characteristic values (eigenvalues) of A.) 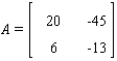
(Multiple Choice)
4.9/5  (33)
(33)
A small firm manufactures bookshelves and desks for microcomputers. For each product it is necessary to use a table saw and a power router. To manufacture each bookshelf, the saw must be used for 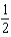 hour and the router for 1 hour. A desk requires the use of each machine for 2 hours. The profits are $20 per bookshelf and $50 per desk. If the saw can be used for 8 hours per day and the router for 12 hours per day, how many bookshelves and desks should be manufactured each day to maximize the profit?
hour and the router for 1 hour. A desk requires the use of each machine for 2 hours. The profits are $20 per bookshelf and $50 per desk. If the saw can be used for 8 hours per day and the router for 12 hours per day, how many bookshelves and desks should be manufactured each day to maximize the profit?
(Multiple Choice)
4.8/5  (38)
(38)
A hospital dietician wishes to prepare a corn-squash vegetable dish that will provide at least 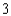 grams of protein and cost no more than
grams of protein and cost no more than 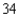 cents per serving. An ounce of creamed corn provides
cents per serving. An ounce of creamed corn provides 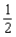 gram of protein and costs
gram of protein and costs 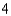 cents. An ounce of squash supplies
cents. An ounce of squash supplies 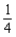 gram of protein and costs
gram of protein and costs 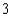 cents. For taste, there must be at least
cents. For taste, there must be at least 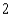 ounces of corn and at least as much squash as corn. It is important to keep the total number of ounces in a serving as small as possible. Find the combination of corn and squash that will minimize the amount of ingredients used per serving.
ounces of corn and at least as much squash as corn. It is important to keep the total number of ounces in a serving as small as possible. Find the combination of corn and squash that will minimize the amount of ingredients used per serving.
(Multiple Choice)
4.9/5  (32)
(32)
Find the determinant of the matrix after introducing zeros. 
(Multiple Choice)
4.9/5  (33)
(33)
A shop specializes in preparing blends of gourmet coffees. From Colombian, Costa Rican, and Kenyan coffees, the owner wishes to prepare 3-pounds bags that will sell for $8.50. The cost per pound of these coffees is $10, $6, and $8, respectively. The amount of Colombian is to be three times the amount of Costa Rican. Find the amount of each type of coffee in the blend.
(Multiple Choice)
4.7/5  (28)
(28)
A stationary company makes two types of notebooks: a deluxe notebook with subject dividers, which sells for $1.2, and a regular notebook, which sells for $0.85. The production cost is $1.00 for each deluxe notebook and $0.75 for each regular notebook. The company has the facilities to manufacture between 2,000 and 3,000 deluxe and between 3,000 and 6,000 regular notebooks, but not more than 8,000 altogether. How many notebooks of each type should be manufactured to maximize the difference between the selling prices and the production cost?
(Multiple Choice)
4.8/5  (31)
(31)
Showing 81 - 100 of 147
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)