Exam 16: Markov Processes

A transition probability describes

Absorbing state probabilities are the same as

A unique matrix of transition probabilities should be developed for each customer.

All Markov chains have steady-state probabilities.

Rent-To-Keep rents household furnishings by the month. At the end of a rental month a customer can: a) rent the item for another month, b) buy the item, or c) return the item. The matrix below describes the month-to-month transition probabilities for 32-inch stereo televisions the shop stocks. 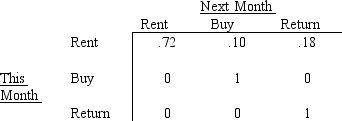What is the probability that a customer who rented a TV this month will eventually buy it?

Analysis of a Markov process

A state i is a transient state if there exists a state j that is reachable from i, but the state i is not reachable from state j.

The probability that the system is in state 2 in the 5th period is $\pi$ ₅(2).

The probability of going from state 1 in period 2 to state 4 in period 3 is

For Markov processes having the memoryless property, the prior states of the system must be considered in order to predict the future behavior of the system.

If a Markov chain has at least one absorbing state, steady-state probabilities cannot be calculated.