Exam 6: Distribution and Network Models
Exam 1: Introduction36 Questions
Exam 2: An Introduction to Linear Programming46 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution36 Questions
Exam 4: Linear Programming Applications in Marketing, Finance, and Operations Management36 Questions
Exam 5: Advanced Linear Programming Applications30 Questions
Exam 6: Distribution and Network Models55 Questions
Exam 7: Integer Linear Programming41 Questions
Exam 8: Nonlinear Optimization Models44 Questions
Exam 9: Project Scheduling: Pertcpm47 Questions
Exam 10: Inventory Models43 Questions
Exam 11: Waiting Line Models40 Questions
Exam 12: Simulation43 Questions
Exam 13: Decision Analysis36 Questions
Exam 14: Multicriteria Decisions39 Questions
Exam 15: Forecasting38 Questions
Exam 16: Markov Processes31 Questions
Select questions type
Consider the following shortest-route problem involving seven cities. The distances between the cities are given below. Draw the network model for this problem and formulate the LP for finding the shortest route from City 1 to City 7.

(Essay)
4.8/5  (40)
(40)
A transshipment constraint must contain a variable for every arc entering or leaving the node.
(True/False)
4.8/5  (36)
(36)
Peaches are to be transported from three orchard regions to two canneries. Intermediate stops at a consolidation station are possible.
 Shipment costs are shown in the table below. Where no cost is given, shipments are not possible. Where costs are shown, shipments are possible in either direction. Draw the network model for this problem.
Shipment costs are shown in the table below. Where no cost is given, shipments are not possible. Where costs are shown, shipments are possible in either direction. Draw the network model for this problem.
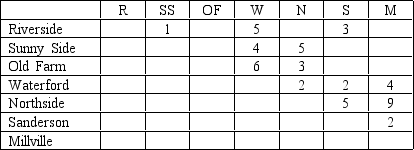
(Essay)
4.9/5  (38)
(38)
The assignment problem is a special case of the transportation problem in which all supply and demand values equal one.
(True/False)
4.8/5  (38)
(38)
In a transportation problem with total supply equal to total demand, if there are four origins and seven destinations, and there is a unique optimal solution, the optimal solution will utilize 11 shipping routes.
(True/False)
4.7/5  (27)
(27)
The following table shows the unit shipping cost between cities, the supply at each source city, and the demand at each destination city. The Management Scientist solution is shown. Report the optimal solution.
 TRANSPORTATION PROBLEM
*****************************
OBJECTIVE: MINIMIZATION
SUMMARY OF ORIGIN SUPPLIES
********************************
TRANSPORTATION PROBLEM
*****************************
OBJECTIVE: MINIMIZATION
SUMMARY OF ORIGIN SUPPLIES
********************************
 SUMMARY OF DESTINATION DEMANDS
***************************************
SUMMARY OF DESTINATION DEMANDS
***************************************
 SUMMARY OF UNIT COST OR REVENUE DATA
*********************************************
SUMMARY OF UNIT COST OR REVENUE DATA
*********************************************
 OPTIMAL TRANSPORTATION SCHEDULE
****************************************
OPTIMAL TRANSPORTATION SCHEDULE
****************************************
 TOTAL TRANSPORTATION COST OR REVENUE IS 1755
TOTAL TRANSPORTATION COST OR REVENUE IS 1755
(Essay)
4.8/5  (33)
(33)
A transportation problem with 3 sources and 4 destinations will have 7 decision variables.
(True/False)
4.8/5  (31)
(31)
Consider a shortest route problem in which a bank courier must travel between branches and the main operations center. When represented with a network,
(Multiple Choice)
4.8/5  (31)
(31)
Transshipment problem allows shipments both in and out of some nodes while transportation problems do not.
(True/False)
5.0/5  (36)
(36)
The direction of flow in the shortest-route problem is always out of the origin node and into the destination node.
(True/False)
4.9/5  (34)
(34)
A transportation problem with 3 sources and 4 destinations will have 7 variables in the objective function.
(True/False)
4.9/5  (28)
(28)
In the general assignment problem, one agent can be assigned to several tasks.
(True/False)
4.8/5  (29)
(29)
A foreman is trying to assign crews to produce the maximum number of parts per hour of a certain product. He has three crews and four possible work centers. The estimated number of parts per hour for each crew at each work center is summarized below. Solve for the optimal assignment of crews to work centers.
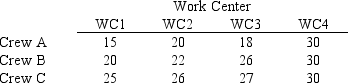
(Essay)
4.9/5  (34)
(34)
Converting a transportation problem LP from cost minimization to profit maximization requires only changing the objective function; the conversion does not affect the constraints.
(True/False)
4.9/5  (33)
(33)
Which of the following is not true regarding an LP model of the assignment problem?
(Multiple Choice)
4.9/5  (31)
(31)
Showing 21 - 40 of 55
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)