Exam 2: An Introduction to Linear Programming
Exam 1: Introduction36 Questions
Exam 2: An Introduction to Linear Programming46 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution36 Questions
Exam 4: Linear Programming Applications in Marketing, Finance, and Operations Management36 Questions
Exam 5: Advanced Linear Programming Applications30 Questions
Exam 6: Distribution and Network Models55 Questions
Exam 7: Integer Linear Programming41 Questions
Exam 8: Nonlinear Optimization Models44 Questions
Exam 9: Project Scheduling: Pertcpm47 Questions
Exam 10: Inventory Models43 Questions
Exam 11: Waiting Line Models40 Questions
Exam 12: Simulation43 Questions
Exam 13: Decision Analysis36 Questions
Exam 14: Multicriteria Decisions39 Questions
Exam 15: Forecasting38 Questions
Exam 16: Markov Processes31 Questions
Select questions type
Muir Manufacturing produces two popular grades of commercial carpeting among its many other products. In the coming production period, Muir needs to decide how many rolls of each grade should be produced in order to maximize profit. Each roll of Grade X carpet uses 50 units of synthetic fiber, requires 25 hours of production time, and needs 20 units of foam backing. Each roll of Grade Y carpet uses 40 units of synthetic fiber, requires 28 hours of production time, and needs 15 units of foam backing.
The profit per roll of Grade X carpet is $200 and the profit per roll of Grade Y carpet is $160. In the coming production period, Muir has 3000 units of synthetic fiber available for use. Workers have been scheduled to provide at least 1800 hours of production time (overtime is a possibility). The company has 1500 units of foam backing available for use.
Develop and solve a linear programming model for this problem.
(Essay)
4.8/5  (35)
(35)
No matter what value it has, each objective function line is parallel to every other objective function line in a problem.
(True/False)
4.8/5  (43)
(43)
A linear programming problem can be both unbounded and infeasible.
(True/False)
4.8/5  (32)
(32)
Find the complete optimal solution to this linear programming problem.
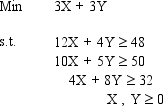
(Essay)
4.8/5  (24)
(24)
In a linear programming problem, the objective function and the constraints must be linear functions of the decision variables.
(True/False)
4.7/5  (31)
(31)
Find the complete optimal solution to this linear programming problem.
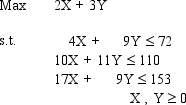
(Essay)
4.8/5  (42)
(42)
For the following linear programming problem, determine the optimal solution by the graphical solution method
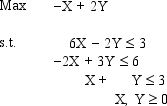
(Essay)
4.9/5  (29)
(29)
Does the following linear programming problem exhibit infeasibility, unboundedness, or alternate optimal solutions? Explain.
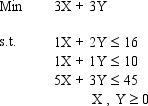
(Essay)
4.8/5  (33)
(33)
Decision variables limit the degree to which the objective in a linear programming problem is satisfied.
(True/False)
4.8/5  (30)
(30)
Alternative optimal solutions occur when there is no feasible solution to the problem.
(True/False)
5.0/5  (32)
(32)
An infeasible problem is one in which the objective function can be increased to infinity.
(True/False)
4.9/5  (33)
(33)
As long as the slope of the objective function stays between the slopes of the binding constraints
(Multiple Choice)
4.9/5  (44)
(44)
Which of the following is a valid objective function for a linear programming problem?
(Multiple Choice)
4.9/5  (41)
(41)
It is possible to have exactly two optimal solutions to a linear programming problem.
(True/False)
4.8/5  (31)
(31)
Only binding constraints form the shape (boundaries) of the feasible region.
(True/False)
4.9/5  (34)
(34)
Showing 21 - 40 of 46
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)