Exam 12: Exponential Functions and Logarithmic Functions
Exam 1: Introduction to Real Numbers and Algebraic Expressions180 Questions
Exam 2: Solving Equations and Inequalities120 Questions
Exam 3: Graphs of Linear Equations82 Questions
Exam 4: Polynomials: Operations115 Questions
Exam 5: Polynomials: Factoring154 Questions
Exam 6: Rational Expressions and Equations125 Questions
Exam 7: Graphs, Functions, and Applications87 Questions
Exam 8: Systems of Equations91 Questions
Exam 9: More on Inequalities98 Questions
Exam 10: Radical Expressions, Equations, and Functions46 Questions
Exam 11: Quadratic Equations and Functions83 Questions
Exam 12: Exponential Functions and Logarithmic Functions68 Questions
Exam 13: Finding Measures of Central Tendency for Prices and Heights57 Questions
Select questions type
Graph the equation of the relation using a solid line, and then graph the inverse of the relation using a dashed line.
-
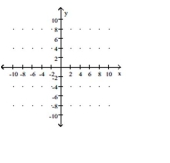
(Multiple Choice)
4.7/5  (28)
(28)
Find the requested composition of functions.
-Given and , find .
(Multiple Choice)
4.8/5  (30)
(30)
Solve the problem.
-An accountant tabulated a firm's profits for four recent years in the following table:
Year Profits 1996 \ 250,000 1997 \ 300,000 1998 \ 400,000 1999 \ 600,000
The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimat profits. Use the linear graph to estimate the profits in the year
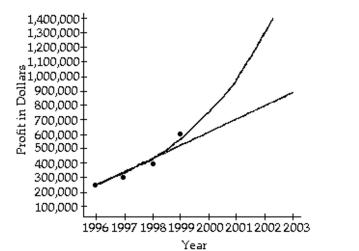
(Multiple Choice)
4.9/5  (37)
(37)
Graph the relation using solid circles and the inverse using open circles.
-
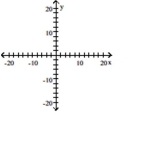
(Multiple Choice)
4.9/5  (40)
(40)
Solve the problem.
-The number of bacteria growing in an incubation culture increases with time according to , where is time in days. Find the number of bacteria when and .
(Multiple Choice)
4.8/5  (43)
(43)
Determine whether the given function is one-to-one. If so, find a formula for the inverse.
-
(Multiple Choice)
4.8/5  (38)
(38)
Find the requested composition of functions.
-Given and , find
(Multiple Choice)
4.8/5  (32)
(32)
Find the requested composition of functions.
-Given and , find .
(Multiple Choice)
4.9/5  (34)
(34)
Find the requested composition of functions.
-Given and , find .
(Multiple Choice)
4.9/5  (36)
(36)
Graph the relation using solid circles and the inverse using open circles.
-
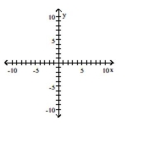
(Multiple Choice)
4.9/5  (34)
(34)
Find the requested composition of functions.
-Given and , find .
(Multiple Choice)
4.9/5  (33)
(33)
Showing 41 - 60 of 68
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)