Exam 12: Sequences, Series, and Probability
Exam 1: Basic Concepts306 Questions
Exam 2: Equations and Inequalities234 Questions
Exam 3: Graphs and Functions61 Questions
Exam 4: Systems of Equations and Inequalities116 Questions
Exam 5: Polynomials and Polynomial Functions112 Questions
Exam 6: Rational Expressions and Equations130 Questions
Exam 7: Roots, Radicals, and Complex Numbers298 Questions
Exam 8: Quadratic Functions221 Questions
Exam 9: Exponential and Logarithmic Functions229 Questions
Exam 10: Characteristics of Functions and Their Graphs142 Questions
Exam 11: Conic Sections132 Questions
Exam 12: Sequences, Series, and Probability208 Questions
Select questions type
Write the first five terms of the sequence whose nth term is shown.
-
(Multiple Choice)
4.9/5  (32)
(32)
Solve the problem.
-A die is rolled. Find the odds against rolling a multiple of 3.
(Multiple Choice)
4.8/5  (39)
(39)
Write the expression for the general (or nth)term,rm, , of the arithmetic sequence.
-
(Multiple Choice)
4.8/5  (34)
(34)
Find the indicated term of the geometric sequence.
-a1 = 4, r = 3; find
(Multiple Choice)
4.9/5  (44)
(44)
Solve the problem.
-The odds against the horse Teabag winning a race are 3:14. i)Find the probability that Teabag wins.
Ii)Find the probability that Teabag loses.
(Multiple Choice)
4.7/5  (33)
(33)
Find the indicated term of the sequence whose nth term is shown.
-
(Multiple Choice)
4.7/5  (26)
(26)
Solve the problem.
-A traffic light is red for 50 seconds, yellow for 5 seconds, and green for 40 seconds. Find the probability: P(the light is not yellow)
(Multiple Choice)
4.9/5  (41)
(41)
Solve the problem.
-A spinner is spun. Assuming that the spinner cannot land on a line, find the probability of landing on a color that is yellow or green. 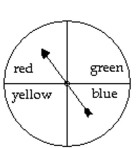
(Multiple Choice)
4.9/5  (39)
(39)
For the given general term an, write an expression using to represent the indicated p to represent the indicated partial sum.
- fifth partial sum
(Multiple Choice)
4.8/5  (34)
(34)
For the geometric sequence, find the common ratio, r.
-2, 0.8, 0.32, 0.128, . . .
(Multiple Choice)
4.7/5  (37)
(37)
Write the expression for the general (or nth)termrm, , of the geometric sequence.
-
(Multiple Choice)
4.7/5  (28)
(28)
Write the word or phrase that best completes each statement or answers the question.
Use mathematical induction to prove the following statement for all positive integers n.
-
(Essay)
4.8/5  (34)
(34)
Write the first five terms of the sequence whose nth term is shown.
-
(Multiple Choice)
4.9/5  (36)
(36)
For the given general term an, write an expression using to represent the indicated p to represent the indicated partial sum.
- third partial sum
(Multiple Choice)
4.7/5  (40)
(40)
Solve the problem.
-A card is selected at random from a deck of cards. Find the probability: P(selecting the 8 of spades)
(Multiple Choice)
4.9/5  (40)
(40)
Showing 81 - 100 of 208
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)