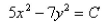Exam 9: Differential Equations
Exam 1: Functions and Models160 Questions
Exam 2: Limits and Derivatives160 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation159 Questions
Exam 5: Integrals160 Questions
Exam 6: Applications of Integration160 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series160 Questions
Exam 12: Vectors and the Geometry of Space159 Questions
Exam 13: Vector Functions160 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals160 Questions
Exam 16: Vector Calculus160 Questions
Exam 17: Second-Order Differential Equations160 Questions
Select questions type
Select the correct Answer: for each question.
-We modeled populations of aphids and ladybugs with a Lotka-Volterra system.Suppose we modify those equations as follows: 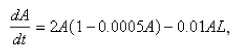
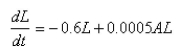 Find the equilibrium solution.
Find the equilibrium solution.
Free
(Multiple Choice)
4.8/5  (31)
(31)
Correct Answer:
D
Suppose that a population develops according to the logistic equation 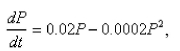 where
where 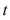 is measured in weeks.What is the carrying capacity?
is measured in weeks.What is the carrying capacity?
Free
(Multiple Choice)
4.8/5  (30)
(30)
Correct Answer:
A
Find the solution of the differential equation that satisfies the initial condition 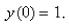
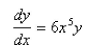
(Essay)
4.9/5  (29)
(29)
A phase trajectory is shown for populations of rabbits  and foxes
and foxes 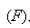 Describe how each population changes as time goes by.
Describe how each population changes as time goes by. 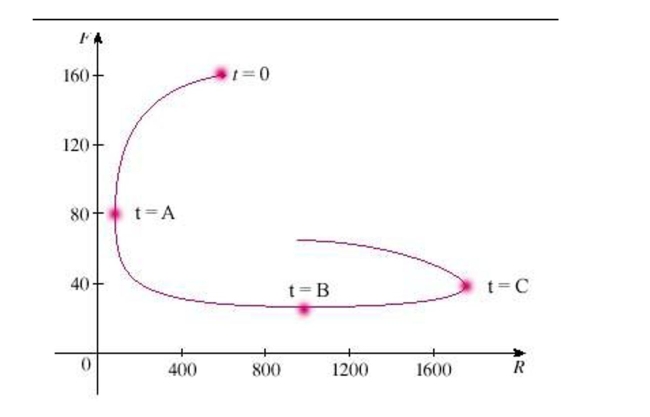 Select the correct statement.
Select the correct statement.
(Essay)
4.7/5  (42)
(42)
A tank contains 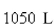 of brine with
of brine with 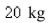 of dissolved salt.Pure water enters the tank at a rate of
of dissolved salt.Pure water enters the tank at a rate of 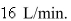 The solution is kept thoroughly mixed and drains from the tank at the same rate.How much salt is in the tank after
The solution is kept thoroughly mixed and drains from the tank at the same rate.How much salt is in the tank after 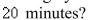
(Essay)
4.9/5  (46)
(46)
Find the solution of the differential equation 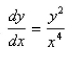 hat satisfies the initial condition
hat satisfies the initial condition 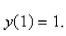
(Essay)
4.9/5  (33)
(33)
The population of the world was about 5.3 billion in 1990.Birth rates in the 1990s range from 35 to 40 million per year and death rates range from 15 to 20 million per year.Let's assume that the carrying capacity for world population is 100 billion.Use the logistic model to predict the world population in the 2,450 year.Calculate yourAnswer in billions to one decimal place.(Because the initial population is small compared to the carrying capacity, you can take 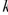 to be an estimate of the initial relative growth rate.) Select the correct Answer
to be an estimate of the initial relative growth rate.) Select the correct Answer
(Multiple Choice)
4.9/5  (37)
(37)
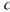 be a positive number.A differential equation of the form
be a positive number.A differential equation of the form 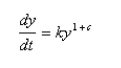 where
where 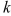 is a positive constant is called
is a positive constant is called 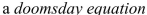 because the exponent in the expression
because the exponent in the expression 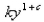 is larger than the exponent 1 for natural growth.An especially prolific breed of rabbits has the growth term
is larger than the exponent 1 for natural growth.An especially prolific breed of rabbits has the growth term 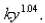 If
If 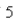 such rabbits breed initially and the warren has
such rabbits breed initially and the warren has 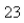 rabbits after
rabbits after 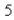 months, then when is doomsday? Select the correct Answer
months, then when is doomsday? Select the correct Answer
(Multiple Choice)
4.9/5  (35)
(35)
Select the correct Answer: for each question.
-A common inhabitant of human intestines is the bacterium 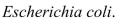 A cell of this bacterium in a nutrient-broth medium divides into two cells every
A cell of this bacterium in a nutrient-broth medium divides into two cells every 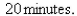 The initial population of a culture is
The initial population of a culture is 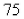 cells.Find the number of cells after
cells.Find the number of cells after 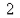 hours.
hours.
(Multiple Choice)
4.7/5  (30)
(30)
A sum of 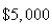 is invested at
is invested at 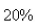 interest.If
interest.If 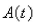 is the amount of the investment at time
is the amount of the investment at time 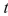 for the case of continuous compounding, write a differential equation and an initial condition satisfied by
for the case of continuous compounding, write a differential equation and an initial condition satisfied by 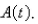
(Essay)
4.9/5  (43)
(43)
Suppose that a population develops according to the logistic equation 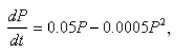 where
where 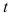 is measured in weeks.What is the carrying capacity?
is measured in weeks.What is the carrying capacity?
(Essay)
4.9/5  (45)
(45)
An object with mass 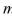 is dropped from rest and we assume that the air resistance is proportional to the speed of the object.If
is dropped from rest and we assume that the air resistance is proportional to the speed of the object.If 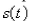 is the distance dropped after t seconds, then the speed is
is the distance dropped after t seconds, then the speed is 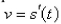 and the acceleration is
and the acceleration is 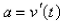 .If g is the acceleration due to gravity, then the downward force on the object is
.If g is the acceleration due to gravity, then the downward force on the object is 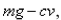 where
where 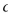 is a positive constant, and Newton's Second Law gives
is a positive constant, and Newton's Second Law gives 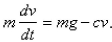 Find the limiting velocity.
Find the limiting velocity.
(Essay)
4.9/5  (36)
(36)
Select the correct Answer: for each question.
-Solve the differential equation. 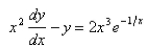
(Multiple Choice)
4.9/5  (33)
(33)
Select the correct Answer: for each question.
-Which of the following functions are the constant solutions of the equation 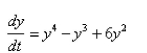 a.
a. 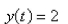 b.
b. 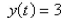 c.
c. 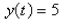 d.
d. 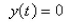 e.
e. 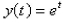
(Short Answer)
4.9/5  (32)
(32)
Showing 1 - 20 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)