Exam 17: Second-Order Differential Equations
Exam 1: Functions and Models160 Questions
Exam 2: Limits and Derivatives160 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation159 Questions
Exam 5: Integrals160 Questions
Exam 6: Applications of Integration160 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series160 Questions
Exam 12: Vectors and the Geometry of Space159 Questions
Exam 13: Vector Functions160 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals160 Questions
Exam 16: Vector Calculus160 Questions
Exam 17: Second-Order Differential Equations160 Questions
Select questions type
Use power series to solve the differential equation.. 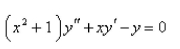
Free
(Essay)
4.8/5  (35)
(35)
Correct Answer:
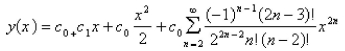
Solve the differential equation using the method of undetermined coefficients. 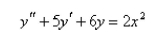
Free
(Multiple Choice)
4.9/5  (41)
(41)
Correct Answer:
E
Solve the differential equation using the method of undetermined coefficients. 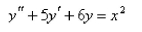
(Essay)
4.8/5  (27)
(27)
Solve the differential equation using the method of variation of parameters. 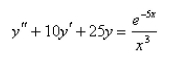
(Essay)
4.8/5  (33)
(33)
A spring with a mass of 2 kg has damping constant 8 and spring constant 80.Graph the position function of the mass at time t if it starts at the equilibrium position with a velocity of 2 m/s.
(Multiple Choice)
4.8/5  (30)
(30)
Suppose a spring has mass M and spring constant k and let 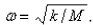 Suppose that the damping constant is so small that the damping force is negligible.If an external force
Suppose that the damping constant is so small that the damping force is negligible.If an external force 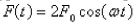 is applied (the applied frequency equals the natural frequency), use the method of undetermined coefficients to find the equation that describes the motion of the mass.
is applied (the applied frequency equals the natural frequency), use the method of undetermined coefficients to find the equation that describes the motion of the mass.
(Essay)
4.8/5  (32)
(32)
Solve the differential equation using the method of variation of parameters. 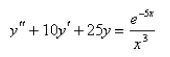
(Essay)
4.8/5  (31)
(31)
The solution of the initial-value problem 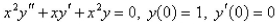 is called a Bessel function of order 0.Solve the initial - value problem to find a power series expansion for the Bessel function.
is called a Bessel function of order 0.Solve the initial - value problem to find a power series expansion for the Bessel function.
(Essay)
4.9/5  (30)
(30)
A 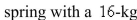 mass has natural length
mass has natural length 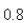 m and is maintained stretched to a length of
m and is maintained stretched to a length of 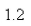 m by a force of
m by a force of 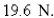 If the spring is compressed to a length of
If the spring is compressed to a length of 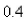 m and then released with zero velocity, find the position
m and then released with zero velocity, find the position 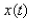 of the mass at any time .
of the mass at any time .
(Essay)
4.8/5  (30)
(30)
Suppose a spring has mass M and spring constant k and let 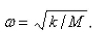 Suppose that the damping constant is so small that the damping force is negligible.If an external force
Suppose that the damping constant is so small that the damping force is negligible.If an external force 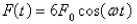 is applied (the applied frequency equals the natural frequency), use the method of undetermined coefficients to find the equation that describes the motion of the mass.
is applied (the applied frequency equals the natural frequency), use the method of undetermined coefficients to find the equation that describes the motion of the mass.
(Multiple Choice)
4.9/5  (36)
(36)
Solve the differential equation using the method of variation of parameters. 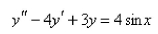
(Essay)
4.8/5  (36)
(36)
A spring with a mass of 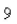 kg has damping constant 28 and spring constant
kg has damping constant 28 and spring constant 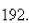 Find the damping constant that would produce critical damping.
Find the damping constant that would produce critical damping.
(Multiple Choice)
4.8/5  (30)
(30)
The solution of the initial-value problem 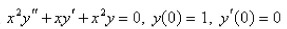 is called a Bessel function of order 0.Solve the initial - value problem to find a power series expansion for the Bessel function.
is called a Bessel function of order 0.Solve the initial - value problem to find a power series expansion for the Bessel function.
(Multiple Choice)
4.8/5  (34)
(34)
Showing 1 - 20 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)