Exam 5: Integrals
Exam 1: Functions and Models160 Questions
Exam 2: Limits and Derivatives160 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation159 Questions
Exam 5: Integrals160 Questions
Exam 6: Applications of Integration160 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series160 Questions
Exam 12: Vectors and the Geometry of Space159 Questions
Exam 13: Vector Functions160 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals160 Questions
Exam 16: Vector Calculus160 Questions
Exam 17: Second-Order Differential Equations160 Questions
Select questions type
Find the integral using the indicated substitution. 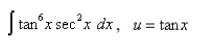
Free
(Essay)
4.9/5  (32)
(32)
Correct Answer:
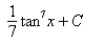
Find the integral using an appropriate trigonometric substitution.Select the correct Answer 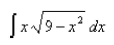
Free
(Multiple Choice)
4.9/5  (37)
(37)
Correct Answer:
B
Find the area of the region that lies to the right of the y-axis and to the left of the parabola 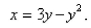
(Essay)
4.8/5  (36)
(36)
Select the correct Answer: for each question.
-Find the indefinite integral 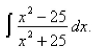
(Multiple Choice)
4.8/5  (28)
(28)
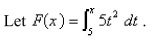 a.Use Part 1 of the Fundamental Theorem of Calculus to find
a.Use Part 1 of the Fundamental Theorem of Calculus to find 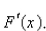 b.Use Part 2 of the Fundamental Theorem of Calculus to integrate
b.Use Part 2 of the Fundamental Theorem of Calculus to integrate 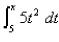 to obtain an alternative expression for
to obtain an alternative expression for 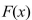 c.Differentiate the expression for
c.Differentiate the expression for 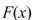 found in part (b).The Fundamental Theorem of Calculus, Part 1 If
found in part (b).The Fundamental Theorem of Calculus, Part 1 If 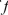 is continuous on [
is continuous on [ 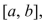 then the function
then the function 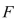 defined by
defined by 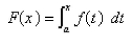
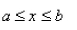 is differentiable on
is differentiable on 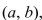 and
and 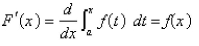 The Fundamental Theorem of Calculus, Part 2 If
The Fundamental Theorem of Calculus, Part 2 If 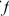 is continuous on
is continuous on 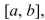 then
then 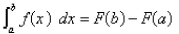 where
where 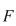 is any antiderivative of that is,
is any antiderivative of that is, 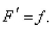
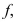
(Essay)
4.8/5  (31)
(31)
If 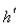 is a child's rate of growth in pounds per year, which of the following expressions represents the increase in the child's weight (in pounds) between the years
is a child's rate of growth in pounds per year, which of the following expressions represents the increase in the child's weight (in pounds) between the years 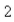 and
and 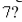
(Essay)
4.8/5  (35)
(35)
By reading values from the given graph of 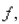 use five rectangles to find a lower estimate, to the nearest whole number, for the area from 0 to 10 under the given graph of
use five rectangles to find a lower estimate, to the nearest whole number, for the area from 0 to 10 under the given graph of 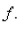
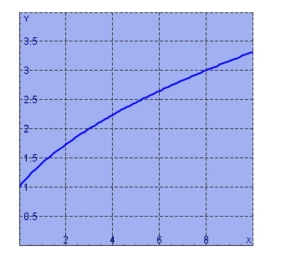
(Short Answer)
4.8/5  (24)
(24)
Find the general indefinite integral.Select the correct Answer 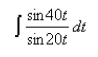
(Multiple Choice)
4.9/5  (35)
(35)
Select the correct Answer: for each question.
-Find the integral. 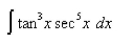
(Multiple Choice)
4.7/5  (34)
(34)
Select the correct Answer: for each question.
-The area of the region that lies to the right of the y-axis and to the left of the parabola 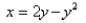 (the shaded region in the figure) is given by the integral
(the shaded region in the figure) is given by the integral 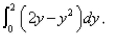 Find the area..
Find the area.. 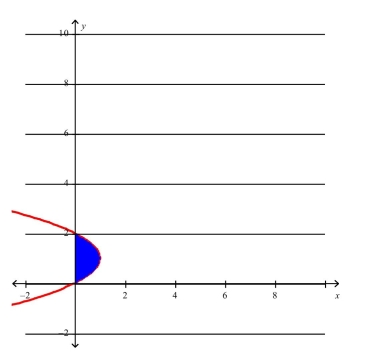
(Multiple Choice)
4.8/5  (38)
(38)
Select the correct Answer for each question.
-Use the following property of the definite integral to estimate the definite integral 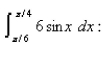
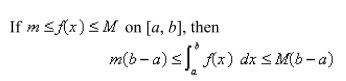
(Multiple Choice)
4.7/5  (37)
(37)
Showing 1 - 20 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)