Exam 11: Sequences, Series, and Probability
Exam 1: Equations, Inequalities, and Modeling531 Questions
Exam 2: Functions and Graphs365 Questions
Exam 3: Polynomial and Rational Functions396 Questions
Exam 4: Exponential and Logarithmic Functions203 Questions
Exam 5: The Trigonometric Functions398 Questions
Exam 6: Trigonometric Identities and Conditional Equations674 Questions
Exam 7: Applications of Trigonometry332 Questions
Exam 8: Systems of Equations and Inequalities293 Questions
Exam 9: Matrices and Determinants218 Questions
Exam 10: The Conic Sections218 Questions
Exam 11: Sequences, Series, and Probability338 Questions
Exam 12: Basic Algebra Review226 Questions
Select questions type
Write the series in summation notation. Use the index i and let i begin at 1 in each summation.
-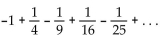
Free
(Multiple Choice)
4.8/5  (43)
(43)
Correct Answer:
A
Solve the problem.
-At a lumber company that sold shelves, a customer could choose from 3 types of wood, 4 different widths and 4 different lengths. How many different types of shelves could be ordered?
Free
(Multiple Choice)
4.9/5  (41)
(41)
Correct Answer:
B
Solve the problem.
-A child on a swing sweeps out a distance of 24 ft on the first pass. If she is allowed to continue swinging until she stops, and if on each pass she sweeps out a distance 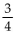 of the previous pass, how far does the child travel?
of the previous pass, how far does the child travel?
(Multiple Choice)
4.9/5  (27)
(27)
Solve the problem.
-Based on meteorological records, the probability that it will snow in a certain town on January 1st is 0.151. Find the probability that in a given year it will not snow on January 1st in that town.
(Multiple Choice)
4.7/5  (33)
(33)
Find the probability of the event.
-If two 12-sided dice are rolled what is the probability that both numbers will be even?
(Multiple Choice)
4.7/5  (34)
(34)
List all equally likely outcomes in the sample space for the indicated experiment.
-A box contains 3 blue cards numbered 1 through 3, and 4 green cards numbered 1 through 4. List the sample space of picking a blue card followed by a green card.
(Multiple Choice)
4.8/5  (29)
(29)
Solve.
-How many different three-digit numbers can be written using digits from the set {2, 3, 4, 5, 6} without any repeating digits?
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-Seven slips of paper marked with the numbers 1, 2, 3, 4, 5, 6, and 7 are placed in a box and mixed well. Two are drawn. What are the odds that the sum of the numbers on the two selected slips is not 6?
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-A bag contains 8 apples and 6 oranges. If you select 7 pieces of fruit without looking, how many ways can you get exactly 6 apples?
(Multiple Choice)
4.8/5  (25)
(25)
Determine whether the statement is true for n = 1, 2, 3, 4, and 5. Use the number of true statements as your answer.
-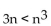
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-What is the coefficient of 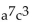 in the expansion of
in the expansion of 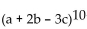
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-An auditorium has 30 rows with 10 seats in the first row, 12 in the second row, 14 in the third row, and so forth. How many seats are in the auditorium?
(Multiple Choice)
4.9/5  (33)
(33)
Write the series in summation notation. Use the index i and let i begin at 1 in each summation.
-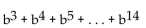
(Multiple Choice)
4.8/5  (22)
(22)
Identify the sequence as arithmetic, geometric, or neither.
-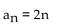
(Multiple Choice)
4.9/5  (39)
(39)
Showing 1 - 20 of 338
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)