Exam 11: Sequences, Series, and Probability
Exam 1: Equations, Inequalities, and Modeling531 Questions
Exam 2: Functions and Graphs365 Questions
Exam 3: Polynomial and Rational Functions396 Questions
Exam 4: Exponential and Logarithmic Functions203 Questions
Exam 5: The Trigonometric Functions398 Questions
Exam 6: Trigonometric Identities and Conditional Equations674 Questions
Exam 7: Applications of Trigonometry332 Questions
Exam 8: Systems of Equations and Inequalities293 Questions
Exam 9: Matrices and Determinants218 Questions
Exam 10: The Conic Sections218 Questions
Exam 11: Sequences, Series, and Probability338 Questions
Exam 12: Basic Algebra Review226 Questions
Select questions type
Solve the problem using the idea of labeling.
-In how many ways can 11 volunteers be assigned to work in the governor's reelection campaign with 3 assigned to stuffing envelopes, 2 assigned to making phone calls, and 6 assigned to making signs?
(Multiple Choice)
4.8/5  (32)
(32)
Use mathematical induction to prove the statement is true for all positive integers n.
-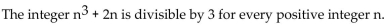
(Essay)
4.8/5  (41)
(41)
Write the repeating decimal number as a fraction.
-0.92929292 . . .
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem using the idea of labeling.
-How many permutations are there of the letters in the word GIGGLE?
(Multiple Choice)
4.7/5  (36)
(36)
Solve the problem.
-The distribution of B.A. degrees conferred by a local college is listed below, by major. 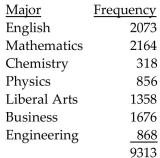 What is the probability that a randomly selected degree is not in Mathematics? Round to the nearest thousandth.
What is the probability that a randomly selected degree is not in Mathematics? Round to the nearest thousandth.
(Multiple Choice)
4.8/5  (44)
(44)
Solve the problem.
-A piece of cardboard is 0.04 in. thick. The cardboard is cut in half, with one half being placed on top of the other so that its thickness doubles for 7 times in a row. How thick would the final stack of cardboard be? Round to
Two decimal places.
(Multiple Choice)
4.9/5  (45)
(45)
Find the sum of the geometric series.
-2 + 6 + 18 + 54 + 162
(Multiple Choice)
4.8/5  (42)
(42)
Solve the problem.
-A collection of dimes is arranged in a triangular array with 12 coins in the base row, 11 in the next, 10 in the next, and so forth with 1 dime in the last row. Find the value of the collection.
(Multiple Choice)
4.8/5  (34)
(34)
Write a recursion formula for the sequence.
--3, 7, 17, 27, . . .
(Multiple Choice)
4.8/5  (46)
(46)
Identify the sequence as arithmetic, geometric, or neither.
--8, 8, -9, 9, -10, 10, . . .
(Multiple Choice)
4.8/5  (42)
(42)
Find the probability of the event.
-A bag contains 6 red marbles, 4 blue marbles, and 1 green marble. What is the probability of choosing a marble that is not blue when one marble is drawn from the bag?
(Multiple Choice)
4.8/5  (31)
(31)
Solve the problem.
-How many 5-card poker hands consisting of 2 aces and 3 kings are possible with an ordinary 52-card deck?
(Multiple Choice)
4.7/5  (35)
(35)
Provide an appropriate response.
-Consider the selection of seven apples from a barrel of 75 apples. Is this a combination, a permutation, or neither?
(Multiple Choice)
4.7/5  (36)
(36)
Write the series in summation notation. Use the index i and let i begin at 1 in each summation.
-4 + 7 + 10 + 13 + 16
(Multiple Choice)
4.9/5  (39)
(39)
Write a formula for the nth term of the arithmetic sequence. Do not use a recursion formula.
-0.23, 0.26, 0.29, 0.32, 0.35, . . .
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-A woman borrowed $20,000 at 8% interest compounded annually. If the loan was paid off in one lump sum at the end of 4 years, how much did she pay?
(Multiple Choice)
4.9/5  (48)
(48)
Showing 41 - 60 of 338
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)