Chat with AIExam 16: Developing and Extending Geometric Concepts and Systems
Give four different types of manipulatives you could use to introduce geometric concepts to elementary children. Explain how these help children to understand these concepts.
(45) 
Answered by Examlex AI Copilot1. Pattern blocks: These are colorful shapes that can be used to create patterns, explore symmetry, and understand the concept of area and perimeter. Children can manipulate the blocks to create different shapes and patterns, helping them to understand geometric concepts in a hands-on way.
2. Geometric solids: These three-dimensional shapes, such as cubes, cones, and cylinders, can help children understand the properties of different shapes and how they can be combined to create more complex figures. By manipulating these solids, children can explore concepts such as volume, surface area, and spatial relationships.
3. Tangrams: Tangrams are a set of seven shapes that can be arranged to form a square. Children can use these shapes to create their own designs and explore concepts such as congruence, symmetry, and transformations. Tangrams also help children develop spatial reasoning and problem-solving skills.
4. Geoboards: Geoboards are square boards with pegs that can be used to create geometric shapes and patterns using rubber bands. By manipulating the rubber bands on the geoboard, children can explore concepts such as angles, symmetry, and the properties of different shapes. This hands-on activity helps children develop a deeper understanding of geometric concepts and spatial relationships.
These manipulatives help children understand geometric concepts by providing them with concrete, visual representations of abstract ideas. By manipulating the shapes and objects, children can explore and experiment with geometric concepts in a way that is engaging and meaningful. This hands-on approach helps children develop a deeper understanding of geometry and build a strong foundation for future mathematical learning.
Explain the differences between congruence and similarity of geometric figures.
(34) Answered by Examlex AI CopilotCongruence and similarity are two different concepts in geometry that describe the relationships between geometric figures.
Congruence refers to the situation where two geometric figures have the same shape and size. In other words, if two figures are congruent, then all corresponding angles are equal and all corresponding sides are equal in length. This means that if you were to superimpose one figure on top of the other, they would perfectly coincide.
On the other hand, similarity refers to the situation where two geometric figures have the same shape but different sizes. In similar figures, corresponding angles are equal, but corresponding sides are proportional in length. This means that if you were to enlarge or shrink one figure, it would become identical to the other.
In summary, congruent figures are identical in shape and size, while similar figures are identical in shape but not in size. Understanding the differences between congruence and similarity is important in geometry, as it helps us to analyze and compare different geometric figures and their properties.
If a fixed figure slides from one position to another, that motion is described as a:
(37) A child who cannot recognize the six parts of a triangle is still operating at which of the following van Hiele levels?
(35) Which of the following triangles can also be an equilateral triangle?
(35) Describing locations of objects with respect to a two- or three- dimensional grid space is a basic concept associated with:
(38) Identifying shapes which have been turned or flipped is a basic concept associated with:
(21) A student contended that if a line cuts a figure into two congruent parts, that line must be a line of symmetry. Is this a true or false statement? Defend your position.
(36) Choosing the highest possible level, a student who can write and understand two-column proofs has reached which van Hiele level?
(31) Teacher Licensing Examination Questions
Praxis: In this circle with center O and radius 2, AP has length 3 and is tangent to the circle at P .
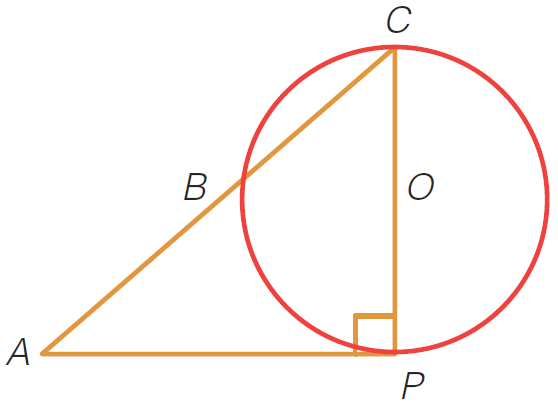If CP is a diameter of the circle, what is the length of AC ?
If CP is a diameter of the circle, what is the length of AC ? (35) The Pythagorean Theorem is useful for all of the following except for :
(43) All of the following statements are true about similar figures except :
(28) An octahedron has 8 faces and 6 vertices. It has ___ edges.
(34) Explain the progression of the van Hiele levels of geometric understanding. Give an example to illustrate each level.
(34) Choosing the highest possible level, a child who recognizes that all squares are rectangles has reached which van Hiele level?
(31) Which of the following reasons is the least valid for including geometry in the elementary school curriculum?
(26) 
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)