Exam 3: Systems of Equations
Exam 1: A Review of Basic Algebra312 Questions
Exam 2: Graphs, Equations of Lines, and Functions286 Questions
Exam 3: Systems of Equations280 Questions
Exam 4: Inequalities193 Questions
Exam 5: Exponents, Polynomials, and Polynomial Functions299 Questions
Exam 6: Rational Expression and Equations297 Questions
Exam 7: Radical Expressions and Equations324 Questions
Exam 8: Quadratic Equations, Functions, and Inequalities132 Questions
Exam 9: Exponential and Logarithmic Functions259 Questions
Exam 10: Conic Sections; More Graphing122 Questions
Exam 11: Miscellaneous Topics102 Questions
Select questions type
represents the equation of a line. Find the value of B so that the line passes through the point (-7,12) .
(Short Answer)
4.9/5  (36)
(36)
Use Cramer s rule to solve the system of equations, if possible. If the equations of the system are dependent, or if the system is inconsistent, so indicate.
(Essay)
4.9/5  (39)
(39)
A student is solving the system by elimination. Which of the following systems is the result if the student wants to eliminate y ?
(Multiple Choice)
4.8/5  (44)
(44)
In the system , equations 1 and 2 were added to eliminate z . Then equation 2 was multiplied by 5 and added to equation 3 to eliminate z . Which of the following systems of equations would be the result?
(Multiple Choice)
4.9/5  (43)
(43)
How many pounds of each candy shown in the illustration must be mixed to obtain 64 pounds of candy that would be worth $4 per pound?
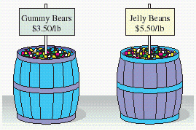 Gummy Bears: __________ lb Jelly Beans: __________ lb
Gummy Bears: __________ lb Jelly Beans: __________ lb
(Short Answer)
4.8/5  (41)
(41)
Determine whether the given ordered triple is a solution of given system.
(Short Answer)
4.9/5  (37)
(37)
Solve the system. If a system is inconsistent or if the equations are dependent, so indicate.
(Essay)
4.8/5  (43)
(43)
Elementary __________ operations are used to produce equivalent matrices that lead to the solution of a system.
(Multiple Choice)
4.8/5  (29)
(29)
Tell whether the ordered pair (3,3) is a solution of the system of equations.
(Multiple Choice)
4.9/5  (43)
(43)
An artist makes three types of ceramic statues at a monthly cost of $655 for 180 statues. The manufacturing costs for the three types are $5, $4, and $3. If the statues sell for $20, $12, and $9, respectively, how many of each type should be made to produce $2,100 in monthly revenue?
__________ expensive, __________ middle-priced, __________ inexpensive
(Short Answer)
4.8/5  (40)
(40)
In the triangle, is more than , and is less than twice . Find each angle in the triangle. ( Hint: The sum of the angles in a triangle is .) 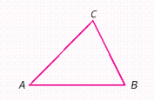
(Multiple Choice)
4.7/5  (40)
(40)
Use Cramer s rule to solve the system of equations, if possible. If the equations of the system are dependent, or if the system is inconsistent, so indicate.
(Short Answer)
4.8/5  (35)
(35)
At the ball park, Sarah can buy 5 hotdogs and 7 hamburgers for $57 or 7 hotdogs and 3 hamburgers for $39. What is the price of a hotdog?
(Short Answer)
4.8/5  (35)
(35)
Solve the system. Give your answer as an ordered triple in the form of ( a, b, c ).
(Multiple Choice)
4.9/5  (34)
(34)
Showing 101 - 120 of 280
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)