Exam 14: Exponential and Logarithmic Functions
Exam 1: Some Basic Concepts of Arithmetic and Algebra255 Questions
Exam 2: The Real Numbers261 Questions
Exam 3: Equations, Inequalities and Problem Solving327 Questions
Exam 4: Formulas and Problem Solving233 Questions
Exam 5: Coordinate Geometry and Linear Systems396 Questions
Exam 6: Exponents and Polynomials390 Questions
Exam 7: Factoring, Solving Equations and Problem Solving302 Questions
Exam 8: A Transition From Elementary Algebra to Intermediate Algebra276 Questions
Exam 9: Rational Expressions277 Questions
Exam 10: Exponents and Radicals274 Questions
Exam 11: Quadratic Equations and Inequalities283 Questions
Exam 12: Coordinate Geometry: Lines, Parabolas, Circles, Ellipses and Hyperbolas165 Questions
Exam 13: Functions195 Questions
Exam 14: Exponential and Logarithmic Functions228 Questions
Exam 15: Systems of Equations: Matrices and Determinants228 Questions
Select questions type
Express as the sum or difference of simpler logarithmic quantities. Assume that all variables represent positive real numbers.
(Short Answer)
4.8/5  (28)
(28)
The change-of-base formula states that if a , b , and r are positive numbers with and , then
(True/False)
4.9/5  (40)
(40)
True or false? The graph below represents a one-to-one function. 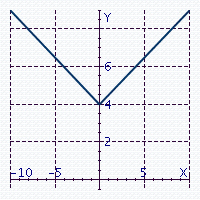
(True/False)
4.8/5  (28)
(28)
Use your calculator to find x when given ln x . Please give the answer to four decimal places.
(Multiple Choice)
4.9/5  (48)
(48)
For a certain strain of bacteria, the number of bacteria present after t hours is given by the equation Q = Q oe0.44 t where Q o represents the initial number of bacteria. How long will it take 400 bacteria to increase to 4,000 bacteria? Express answer to the nearest tenth without the units. __________ hours
(Short Answer)
4.8/5  (31)
(31)
Form the inverse function f - -1, and list the domain and range of f - -1. f = {(1, 6), (4, 8), (6, 50)} Match the name of each set with the corresponding set.
-
(Multiple Choice)
4.9/5  (35)
(35)
Use a calculator to find each common logarithm. Express answer to four decimal places.
(Multiple Choice)
4.9/5  (28)
(28)
Use the formulas or to find the amount for the investment. $4,200 for 5 years at 5% compounded continuously.
(Multiple Choice)
4.7/5  (29)
(29)
Form the inverse function f - -1, and list the domain and range of f - -1. f = {(0, 0), (2, 6), (-1, -1), (-2, -6)} Match the name of each set in the left column with the corresponding set in the right column.
-
(Multiple Choice)
4.8/5  (35)
(35)
Use the formula to find the amount for the investments. $13,600 for 5 years at 4.5% compounded semiannually. Please round the answer to the nearest cent. $__________ $13,600 for 5 years at 4% compounded monthly. Please round the answer to the nearest cent. $__________ Determine which investment amounts to more. __________
(Short Answer)
4.9/5  (28)
(28)
For a certain culture the equation , where Q 0 is an initial number of bacteria and t is time measured in hours, yields the number of bacteria as a function of time. How long will it take 700 bacteria to increase to 2,800? Please enter the answer as a number without the units and round to the nearest tenth. __________ hours
(Short Answer)
4.7/5  (39)
(39)
Showing 41 - 60 of 228
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)