Exam 9: Binomial Distribution
Exam 1: Statistics and Scientific Method102 Questions
Exam 2: Basic Mathematical and Measurement Concepts110 Questions
Exam 3: Frequency Distributions116 Questions
Exam 4: Measures of Central Tendency and Variability125 Questions
Exam 5: The Normal Curve and Standard Scores105 Questions
Exam 6: Correlation139 Questions
Exam 7: Linear Regression101 Questions
Exam 8: Random Sampling and Probability123 Questions
Exam 9: Binomial Distribution121 Questions
Exam 10: Introduction to Hypothesis Testing: Using the Sign Test141 Questions
Exam 11: Power103 Questions
Exam 12: Sampling Distributions, Sampling Distribution of the Mean: the Normal Deviate Z Test135 Questions
Exam 13: Students T Test for Single Samples121 Questions
Exam 15: Introduction to the Analysis of Variance218 Questions
Exam 16: Introduction to the Two-Way Analysis of Variance115 Questions
Exam 17: Chi-Square and Other Nonparametric Tests170 Questions
Select questions type
One can appropriately apply the binomial distribution if P = 0.5 and Q = 0.3 in a problem.
(True/False)
4.7/5  (36)
(36)
What is the probability of tossing 8 unbiased coins once and obtaining at least 5 heads?
(Short Answer)
4.8/5  (38)
(38)
To use the normal approximation, it is required that either NP ?5= 10 or NQ ?5= 10, but not both.
(True/False)
4.8/5  (32)
(32)
In order to use the binomial distribution, which of the following conditions are necessary?
(Multiple Choice)
4.8/5  (26)
(26)
In order to correctly apply the binomial distribution, one of the conditions that must be met is that there are only two possible outcomes on each trial.
(True/False)
4.9/5  (31)
(31)
The binomial distribution requires that the P and Q do not change from trial-to-trial.
(True/False)
4.8/5  (35)
(35)
To apply the binomial distribution properly ( P + Q ) must equal 1.00.
(True/False)
4.7/5  (34)
(34)
A true-false test of 20 questions is given to 10,000 students. If all the students guess on each question, how many students would you expect to get 17 or more questions correct?
(Multiple Choice)
4.9/5  (38)
(38)
In the binomial expansion of ( P + Q ) 10 , the last term of the expansion will be _________.
(Multiple Choice)
4.9/5  (37)
(37)
The binomial distribution requires that P and Q stay the same from trial-to-trial.
(True/False)
4.8/5  (31)
(31)
If one flips 5 unbiased coins once, what is the probability of getting exactly 3 heads?
(Multiple Choice)
4.9/5  (37)
(37)
A tea manufacturer believes his company's tea (Tea A) has a very distinctive taste. He conducts a study to evaluate his believe. Five employees are asked to taste Tea A and two other tea's once, in random order and to try to identify which tea was Tea A. All five employees correctly identify Tea A. These results are encouraging. More quantitatively, according to the binomial distribution, if chance alone is at work, what is the probability of getting this outcome? If the tea manufacturer conducted another study similar to this one, give three things the manufacturer could do to alter the study so that if Tea A is really responsible for the result, rather than chance alone, he could have more confidence in the outcome. Assume good experimental design was followed in the original experiment.
(Essay)
4.9/5  (31)
(31)
Develop the binomial distribution for the experiment of tossing 3 unbiased coins once. Use the following table to help you set up the problem. 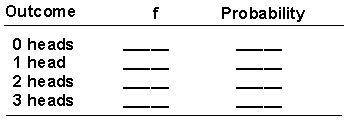
(Not Answered)
This question doesn't have any answer yet
The probability of getting a result as extreme or more extreme than 5 heads out of a toss of 7 unbiased coins is 0.4532.
(True/False)
4.8/5  (39)
(39)
Consider the binomial expansion for 6 events: P 6 + 6 P 5 Q + 15 P 4 Q 2 + 20 P 3 Q 3 + 15 P 2 Q 4 + 6 PQ 5 + Q 6 What term would you use in evaluating the probability of obtaining exactly 2 heads as the result of flipping an unbiased coin 6 times?
(Multiple Choice)
4.9/5  (35)
(35)
If the conditions for the binomial distribution are met, P + Q must equal 1. Is this true? Why?
(Essay)
4.8/5  (32)
(32)
For the binomial distribution to be applicable to a situation,
(Multiple Choice)
4.7/5  (38)
(38)
Showing 21 - 40 of 121
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)