Exam 13: Analysis of Variance: Factorial Design

If you add the number of independent variables and dependent variables in a 2 x 2 factorial ANOVA, the sum is

The effect size index, d, can be used on factorial ANOVA problems.

In a 6 x 7 factorial design with three observations per cell, the df for the interaction F would be

Consider a factorial ANOVA that analyzes self esteem scores. Three different ages participate: 20 year-olds, 40 year-olds, and 60 year-olds. In addition, each age group is divided into those who have above a median income and those who have below a median income. The researchers concluded that the differences in self esteem scores of the different age groups did not depend on a person's income. The summary table for the factorial ANOVA would certainly show that there was

Data Set 13-9: Each point represents a mean based on 5 scores. 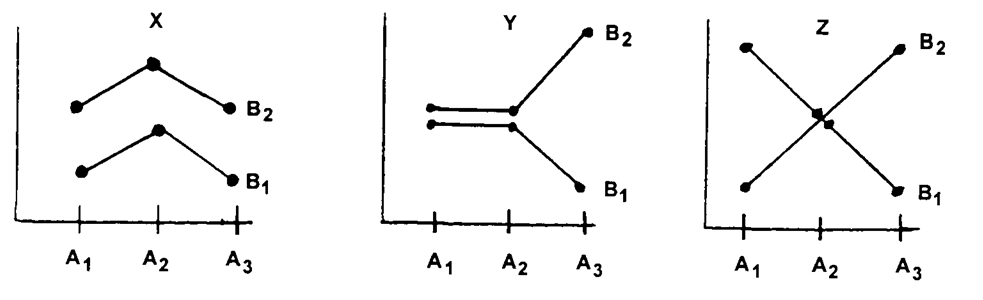-The data in Data Set 13-9 are all examples of afactorial ANOVA.

Data Set 13-4: The number in each cell is the mean of 5 participants on the Loose Label Political Opinion Poll (high scores = liberal, low scores = conservative). $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$$\text { Socioeconomic Status }$ Low Medium High Major in Humanities 50 20 50 College Nat. Science 30 60 30 -Data Set 13-4 is an example of

A significant interaction is characterized by parallel lines.

A interaction that is not significant is characterized by parallel lines.

A mental health clinic analyzed "improvement scores"for 40 clients. Twenty were college students who had seen either a cognitive/behavioral therapist or a client-centered therapist. The other 20 were 17-21 years old but not in college, and they too were evenly divided between the kinds of therapists. The tables below give the mean improvement score for each group and a summary of the ANOVA. Tell what the study shows. College Non-College Kind of cognitive/ behavioral 12 18 Therapist client-centered 25 17 Source df MS F Therapists 1 68.24 5.07 Clients 1 9.69 0.72 AB 1 123.16 9.15 Error 36 13.46

A histogram of a significant interaction shows stairs with steps that are about equal.

Which of the following is (are) true?

For both one-way ANOVA and factorial ANOVA, the restrictions and limitations include

The factorial ANOVA described in Chapter 13 is appropriate when the cells have an equal number of scores.

Designs that are equal in the number of factors are

A factorial ANOVA and an independent-samples t test have the same

Inspired by the problem in your text of students who were paid to write essays in support of the police, Lepper, Greene and Nisbett had nursery school children color with Magic Markers. Some children expected to be rewarded and some did not. In addition, half the children received a reward and half did not. Afterward, the children were tested for their interest in coloring with Magic Markers. High scores mean greater interest. Analyze the data and write an explanation of the results. Expected a Reward Yes No 6 13 Received a Yes 5 10 Reward 2 14 15 16 No 11 14 13 11

If the interaction is significant, the main effects can be interpreted as if they came from a one-way ANOVA.

In a 2 x 3 factorial design with five participants per cell, the df for the interaction F would be

Data Set 13-8: N = 10 for each cell. 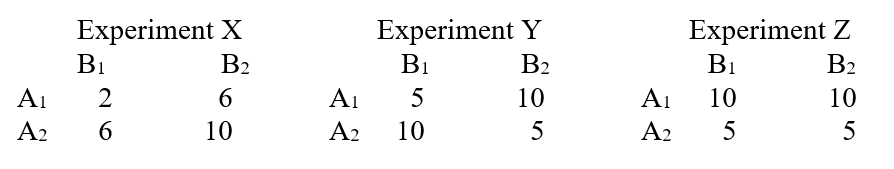-The F value for the interaction in Experiment X of Data Set 13-8 is based on degrees of freedom of and .

A 3 x 5 factorial ANOVA with five scores per cell produced a MS_AB = 80 and a MS_error = 40. For the factor with 3 levels and $\alpha$ = .05, a Tukey HSD would