Exam 13: Analysis of Variance: Factorial Design

An interaction occurs when one main effect in a factorial ANOVA is significant but the second one is not.

Data Set 13-3: 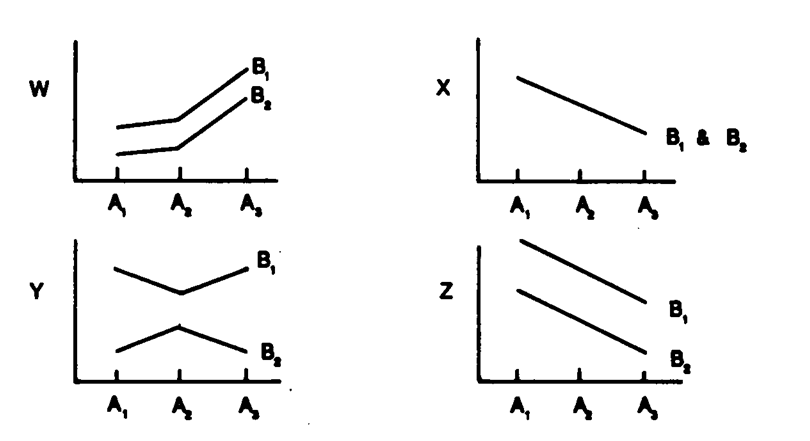-Refer to Data Set 13-3. The figure that shows an interaction is

From a factorial ANOVA with factors A and B, you can determine if

Which of the following is true for factorial ANOVA but not true for one-way ANOVA?

Parents learn tricks that are helpful in raising children and in preserving the sanity of all concerned. When a baby is crying, just changing diapers will stop crying 25 percent of the time. Picking the baby up and walking stops crying 40 percent of the time. Suppose a (desperate?) parent did both. Which outcome (percent) would indicate that the effect of the two tricks is independent, that they do not interact?

With respect to the number of independent variables, which of these designs is not like the others?

Consider a factorial ANOVA in which the dependent variable is reaction time scores. Three different drugs are tested on both females and males. The researchers concluded that the effect of a drug did not depend on whether the person taking it was a female or male. The factorial ANOVA would certainly show that

In a factorial ANOVA, df_tot is equal to

Mr. Jefferson, a farmer-philosopher-president, has a vineyard. On his fields 5-10-5 fertilizer (5 percent nitrogen, 10 percent potash, 5 percent potassium) causes a 10 percent increase in yield of corn. 10-20-10 fertilizer causes a 15 percent increase in yield of corn. Suppose both fertilizers were applied by Mr. Jefferson (whose philosophy is, "If a little bit does a little good, a whole lot will do a whole lot of good"). Which outcome below would indicate if there was no interaction?

If the interaction is not significant, the main effects can be interpreted as if they came from a one-way ANOVA.

Restrictions and limitations for both one-way ANOVA and factorial ANOVA include

Data Set 13-7: A political scientist reported a study on attitudes toward increasing military expenditures. The attitudes of four groups were reported: US Army officers, corporate managers, public school teachers, and assembly-line workers. Within each of the categories, those under age 35 were tabulated separately from those over 35. A factorial ANOVA on the data produced a significant interaction; the main effect for age was not significant. -Which of the following is a possible conclusion from Data Set 13-7?

Data Set 13-4: The number in each cell is the mean of 5 participants on the Loose Label Political Opinion Poll (high scores = liberal, low scores = conservative). $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$$\text { Socioeconomic Status }$ Low Medium High Major in Humanities 50 20 50 College Nat. Science 30 60 30 -In Data Set 13-4, the interaction appears to be

Which of the following is (are) true?

A 3 x 5 factorial ANOVA has independent variables.

In a 4 x 4 factorial design with five subjects per cell, the df for the interaction F would be

In a 4 x 5 factorial design with nine participants per cell, the df for the interaction F would be

Data Set 13-2 Numbers in the cell are means based on 8 scores for each cell. A 10 20 30 B 40 50 60 50 30 10 -In Data Set 13-2 the main effect of A appears to be

For her Research Methods project, Laura presented undergraduate men and women with a scenario that described a person confronted with problems that were described in detail. Half the scenarios included the additional information that a panel of male experts had provided a list of solutions to the problems the person faced. After reading the scenario, the participants described to Laura how they would respond. From transcripts of their descriptions, Laura scored each person's response for both solutions and for empathy. The solution scores are shown below. Analyze them and write a conclusion about the experiment. Scenario Additional Information Control 12 8 14 7 Women 10 5 Gender 11 7 9 15 6 11 Men 5 14 6 13

In testing for a main effect using a factorial ANOVA, the null hypothesis is that the populations from which the samples were drawn