Exam 12: Vectors and Matrices
Exam 1: Linear Functions and Change125 Questions
Exam 2: Functions107 Questions
Exam 3: Quadratic Functions41 Questions
Exam 4: Exponential Functions102 Questions
Exam 5: Logarithmic Functions79 Questions
Exam 6: Transformations of Functions and Their Graphs100 Questions
Exam 7: Trigonometry in Circles and Triangles120 Questions
Exam 8: Trigonometric Functions120 Questions
Exam 9: Trigonometric Identities and Their Applications60 Questions
Exam 10: Compositions, Inverses, and Combinations of Functions64 Questions
Exam 11: Polynomial and Rational Functions143 Questions
Exam 12: Vectors and Matrices102 Questions
Exam 13: Sequences and Series81 Questions
Exam 14: Parametric Equations and Conic Sections120 Questions
Select questions type
A car travels 19 miles south and then 24 miles east. Which of the following is true?
(Multiple Choice)
4.8/5  (39)
(39)
Three people stand in the middle of a field. The first person walks 11 yards north and then 14 yards east. The second person remains where he is. The third person walks 18 yards north and then 8 yards east. The angle formed by drawing a line from the first person to the second person to the third person is _____  . Round to the nearest whole number.
. Round to the nearest whole number.
(Short Answer)
4.7/5  (34)
(34)
An airplane is flying at an airspeed of 660 km/hr in a crosswind blowing from the southeast at a speed of 60 km/hr. To end up going due east, the plane should head _____  south of east and will have a speed of ______km/hr relative to the ground. Round each answer to 2 decimal places.
south of east and will have a speed of ______km/hr relative to the ground. Round each answer to 2 decimal places.
(Short Answer)
4.8/5  (32)
(32)
A retailer's total monthly sales of three different models of television is given by the vector 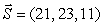 . If the sales for each model go up by 8 the next month, what is
. If the sales for each model go up by 8 the next month, what is 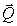 , the next month's total sales?
, the next month's total sales?
(Short Answer)
4.9/5  (35)
(35)
Jack and Jill begin walking away from a water well. Jill walks 6 meters north, and then 12 meters northeast. When Jill stops, Jack is half as far from the well as she is. How far is Jack from the well?
(Short Answer)
4.8/5  (43)
(43)
In certain cases, there is a nonzero vector 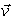 and a scalar
and a scalar 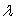 for a matrix
for a matrix 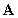 such that
such that 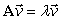 . The vector
. The vector 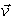 is called an eigenvector of
is called an eigenvector of 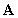 with eigenvalue
with eigenvalue 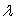 . Let
. Let 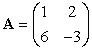 with eigenvector
with eigenvector 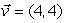 . What is its eigenvalue?
. What is its eigenvalue?
(Short Answer)
4.8/5  (44)
(44)
The vector starting at the point P = (0, 2) and ending at the point Q = (1, 4) can be resolved into the components 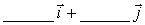
(Short Answer)
5.0/5  (28)
(28)
Let 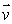 be a vector of length 3 pointing
be a vector of length 3 pointing 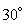 north of east. Find the length and direction of
north of east. Find the length and direction of 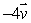 .
.
(Short Answer)
4.7/5  (31)
(31)
A country has two main political parties. The vector 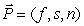 Gives the number of people who are members of the first party, the second party, and neither party, respectively. Suppose
Gives the number of people who are members of the first party, the second party, and neither party, respectively. Suppose
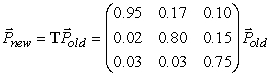 . Which party's members are the most loyal?
. Which party's members are the most loyal?
(Multiple Choice)
4.8/5  (42)
(42)
Let the vector 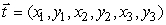 describe a triangle with vertices at
describe a triangle with vertices at 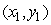 ,
, 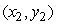 , and
, and 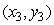 . If the triangle
. If the triangle 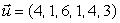 is rotated through an angle of 28
is rotated through an angle of 28 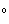 clockwise about the origin, what is the resulting vector? Round each entry to 2 decimal places.
clockwise about the origin, what is the resulting vector? Round each entry to 2 decimal places.
(Short Answer)
4.7/5  (40)
(40)
The inverse of a matrix 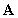 , denoted by
, denoted by 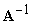 , is such that if
, is such that if 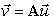 , then
, then 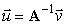 . For a matrix
. For a matrix 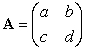 , the inverse
, the inverse 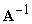 is given by
is given by 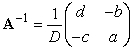 , where
, where 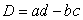 .
. 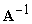 is undefined if D = 0. Let
is undefined if D = 0. Let 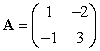 . Does
. Does 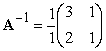 ?
?
(True/False)
4.9/5  (45)
(45)
Showing 21 - 40 of 102
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)