Exam 4: Lossless Compression Algorithms

Consider an alphabet with three symbols $A, B, C$ , with probability $P(A)=x, P(C)=y$ . and $P(C)=1-x-y$ . State how you would go about plotting the entropy as a function of $x$ and $y$ . Pseudocode is perhaps the best way to state your answer.

Free

(Essay)

4.9/5

(33)

Question 1

Correct Answer:

Verified

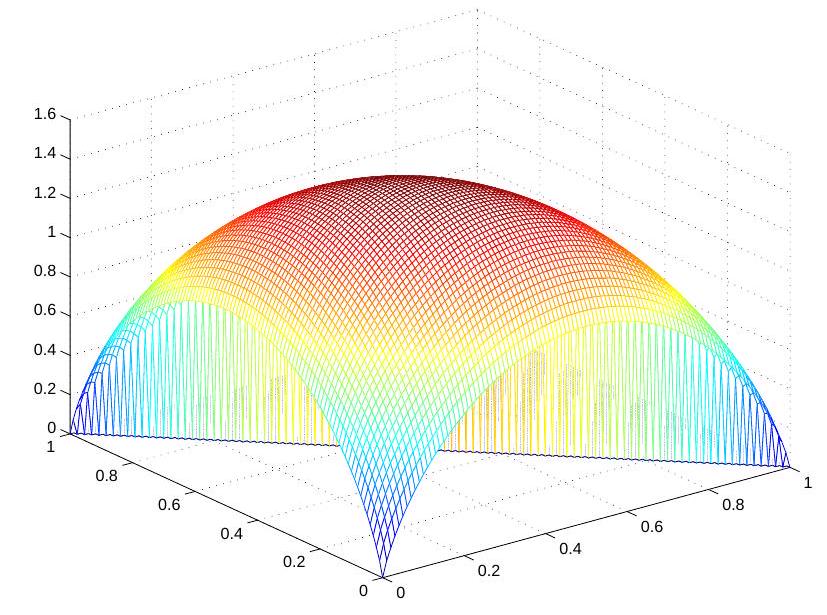
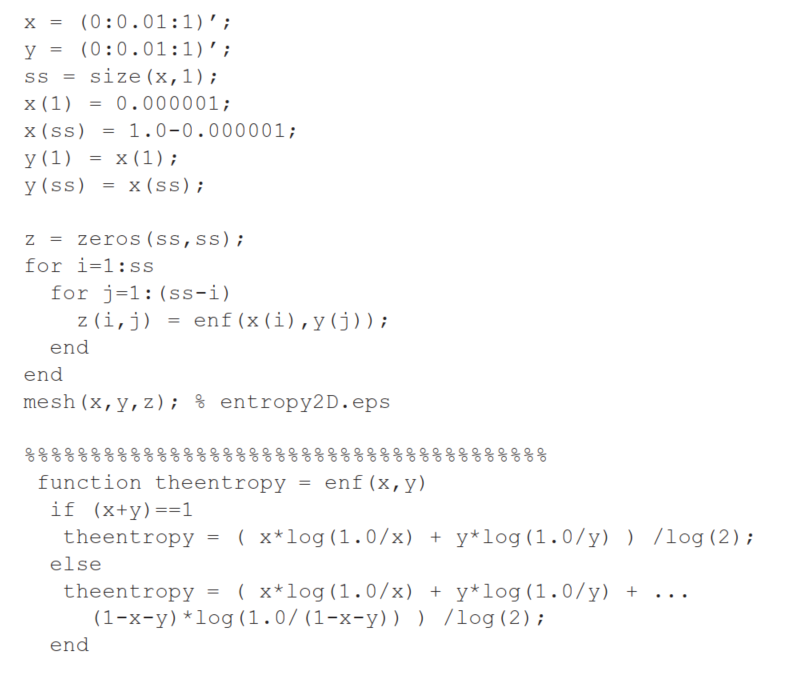
matlab:

If the source string MULTIMEDIA is now encoded using Arithmetic coding, what is the codeword in fractional decimal representation. How many bits are needed for coding in binary format? How does this compare to the entropy?

Free

(Essay)

4.7/5

(38)

Question 2

Correct Answer:

Verified

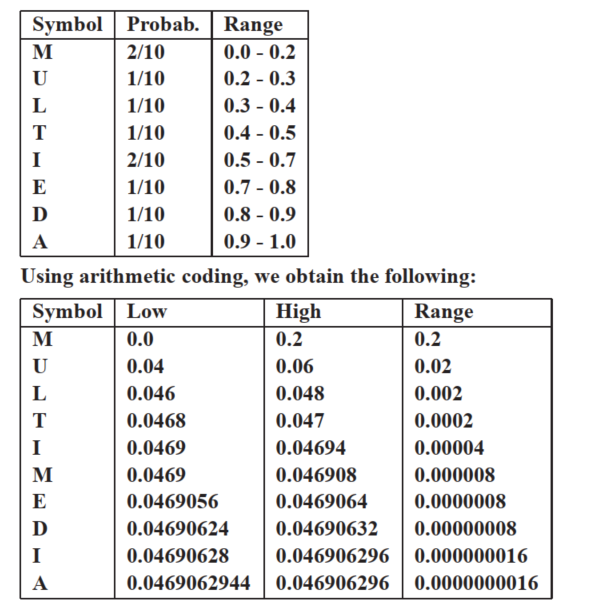
$We need \log _{2}(r) bits to code the sequence of symbols, where r is the range for the last coded symbol. Here, r is \mathbf{0.0000000016} , so the result is then computed as \mathbf{29.21928095} and the average bits per symbol equals 2.921928095 . We note that this is exactly equal to the entropy of the source, so in this case arithmetic coding provides optimal performance.$
We need $\log _{2}(r)$ bits to code the sequence of symbols, where $r$ is the range for the last coded symbol. Here, $r$ is $\mathbf{0.0000000016}$ , so the result is then computed as $\mathbf{29.21928095}$ and the average bits per symbol equals 2.921928095 . We note that this is exactly equal to the entropy of the source, so in this case arithmetic coding provides optimal performance.

Construct a binary Huffman code for a source $S$ with three symbols $A, B$ and $C$ , having probabilities $0.6,0.3$ , and 0.1 , respectively. What is its average codeword length, in bits per symbol? What is the entropy of this source? (b) Let's now extend this code by grouping symbols into 2-character groups - a type of VQ. Compare the performance now, in bits per original source symbol, with the best possible. 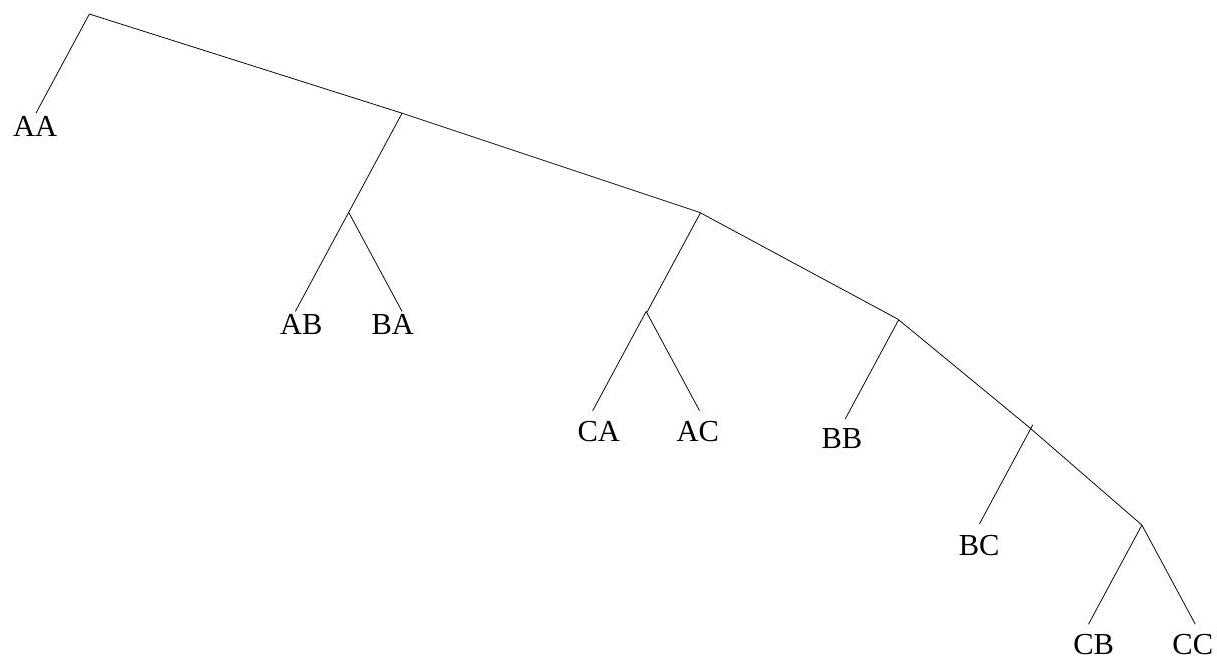Fig. 7.1:

Free

(Essay)

4.7/5

(34)

Question 3

Correct Answer:

Verified

(a) A: 1; B: 00; C: 01;
Average $=0.1 * 2+0.3 * 2+0.6 * 1=1.4$ bits/symbol
Entropy $=-$ sum $p_{i} \log p_{i}=\mathbf{1 . 2 9 5 5}$
(b) Tree is per Fig. 7.1.
Codeword bitlengths are:
$(a) A: 1; B: 00; C: 01; Average =0.1 * 2+0.3 * 2+0.6 * 1=1.4 bits/symbol Entropy =- sum p_{i} \log p_{i}=\mathbf{1 . 2 9 5 5} (b) Tree is per Fig. 7.1. Codeword bitlengths are: 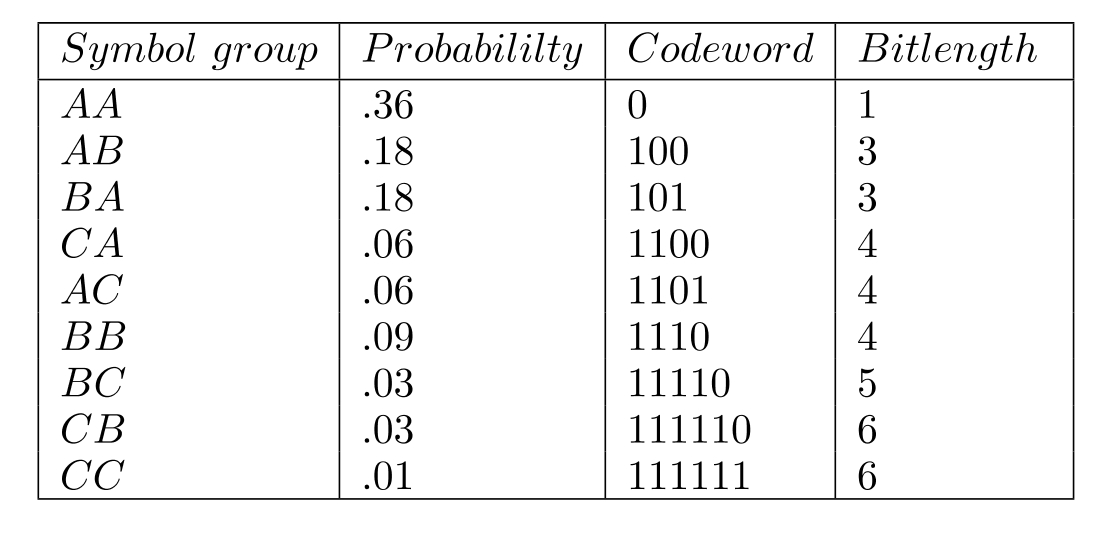Average =0.5 *(0.36+3 \times 0.18+3 \times 0.18+4 \times 0.09+4 \times 0.06+4 \times 0.06+5 \times 0.03+6 \times 0.03+6 \times 0.01) =1.3350 The best possible is the entropy, given by: H=-0.1 \lg (0.1)+-0.3 \lg (0.3)-0.6 \lg (0.6)=1.2954618$ Average $=0.5 *(0.36+3 \times 0.18+3 \times 0.18+4 \times 0.09+4 \times 0.06+4 \times 0.06+5 \times 0.03+6 \times 0.03+6 \times 0.01)$ $=1.3350$
The best possible is the entropy, given by: $H=-0.1 \lg (0.1)+-0.3 \lg (0.3)-0.6 \lg (0.6)=1.2954618$

For the LZW algorithm, assume an alphabet $\{$ a b o d $\}$ of size 5 from which text characters are picked. Suppose the following string of characters is to be transmitted (or stored): $\mathrm{dabba} \mathrm{dabba} * \mathrm{dabba} * \mathrm{doo} * \mathrm{doo} \ldots$ The coder starts with an initial dictionary consisting of the above 5 characters and an index assignment, as in the following table: $For the LZW algorithm, assume an alphabet \{* a b o d \} of size 5 from which text characters are picked. Suppose the following string of characters is to be transmitted (or stored): \mathrm{dabba} * \mathrm{dabba} * \mathrm{dabba} * \mathrm{doo} * \mathrm{doo} \ldots The coder starts with an initial dictionary consisting of the above 5 characters and an index assignment, as in the following table: 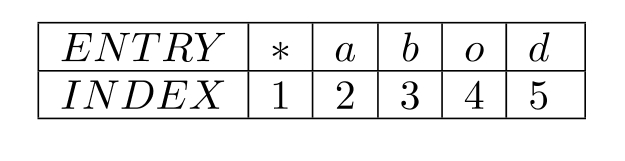Make a table showing the string being assembled, the current character, the output, the new symbol, and the index corresponding to the symbol, for the above input - only go as far as d a b b a d a b b a * d.$ Make a table showing the string being assembled, the current character, the output, the new symbol, and the index corresponding to the symbol, for the above input - only go as far as "d a b b a d a b b a * d".

(Essay)

4.9/5

(30)

Question 4

Consider a text string containing a set of characters and their frequency counts as follows: A: (15), B: (7), C: (6), D: (6) and E: (5). Show that the Shannon-Fano algorithm produces a tree that encodes this string in a total of 89 bits, whereas the Huffman algorithm needs only 87 bits.

(Essay)

4.8/5

(40)

Question 5

Suppose we have a source consisting of two symbols, $X$ and $Y$ , with probabilities $P_{X}=2 / 3$ and $P_{Y}=1 / 3$ . (a) Using Arithmetic Coding, what are the resulting bitstrings, for input $XXX$ and $YXX$ ? (b) A major advantage of adaptive algorithms is that no a priori knowledge of symbol probabilities is required. (1) Propose an Adaptive Arithmetic Coding algorithm and briefly describe how it would work. For simplicity, let's assume both encoder and decoder know that exactly $k=3$ symbols will be sent each time. (2) Assume the sequence of messages is initially $3 XXX \mathrm{~s}$ , followed by $11 YYY \mathrm{~s}-$ the sequence is $X X X X X X X X X Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y$ $Y Y Y$ . Show how your Adaptive Arithmetic Coding algorithm works, for this sequence, for encoding: (i) the first $XXX$ , (ii) the second $XXX$ , and (iii) the last $YYY$ .

(Essay)

4.7/5

(34)

Question 6

Calculate the entropy of a "checkerboard" image in which half of the pixels are BLACK and half of them are WHITE.

(Essay)

4.8/5

(44)

Question 7

Consider the question of whether it is true that the size of the Huffman code of a symbol $a_{i}$ with probability $p_{i}$ is always less than or equal to $\left\lceil-\log p_{i}\right\rceil$ . As a counter example, let the source alphabet be $\{=a, b\}$ . Given $p(a)$ and $p(b)$ , construct a Huffman tree. Will the tree be different for different values for $p(a)$ and $p(b)$ ? What conclusion can you draw?

(Essay)

4.8/5

(36)

Question 8

Using the Lempel-Ziv-Welch (LZW) algorithm, encode the following source symbol sequence: MISSISSIPPI\# Show initial codes as ASCII: e.g., "M". Start new codes with the code value 256. (b) Assuming the source characters (ASCII) and the dictionary entry codes are combined and represented by a 9-bit code, calculate the total number of bits needed for encoding the source string up to the \# character, i.e. just MISSISSIPPI. What is the compression ratio, compared to simply using 8-bit ASCII codes for the input characters?

(Essay)

4.9/5

(42)

Question 9

Is the following code uniquely decodable? 1 \mapstoa 2 \mapstoaba 3 \mapstobab

(Essay)

4.9/5

(43)

Question 10

Suppose we wish to transmit the 10-character string "MULTIMEDIA". The characters in the string are chosen from a finite alphabet of 8 characters. (a) What are the probabilities of each character in the source string? (b) Compute the entropy of the source string. (c) If the source string is encoded using Huffman coding, draw the encoding tree and compute the average number of bits needed.

(Essay)

4.9/5

(29)

Question 11

Showing 1 - 11 of 11

Consider an alphabet with three symbols $A, B, C$ , with probability $P(A)=x, P(C)=y$ . and $P(C)=1-x-y$ . State how you would go about plotting the entropy as a function of $x$ and $y$ . Pseudocode is perhaps the best way to state your answer.

If the source string MULTIMEDIA is now encoded using Arithmetic coding, what is the codeword in fractional decimal representation. How many bits are needed for coding in binary format? How does this compare to the entropy?

Consider a text string containing a set of characters and their frequency counts as follows: A: (15), B: (7), C: (6), D: (6) and E: (5). Show that the Shannon-Fano algorithm produces a tree that encodes this string in a total of 89 bits, whereas the Huffman algorithm needs only 87 bits.

Calculate the entropy of a "checkerboard" image in which half of the pixels are BLACK and half of them are WHITE.

Is the following code uniquely decodable? 1 \mapstoa 2 \mapstoaba 3 \mapstobab

Multimedia Authoring, Tools, Graphics and Image Data Representations

Color in Image and Video

Fundamental Concepts in Video and Basics of Digital Audio

Lossy Compression Algorithms, Image Compression Standards and Basic Video Compression Techniques

Mpeg Video Coding I -- Mpeg-1 and 2, Basic Audio Compression Techniques, Mpeg Audio Compression, Computer and Multimedia Networks

Multimedia Network Communications and Applications, Wireless Networks and Content-Based Retrieval in Digital Libraries

Filters