Exam 7: Multimedia Network Communications and Applications, Wireless Networks and Content-Based Retrieval in Digital Libraries

To makes matters simpler for eventual printing, we buy a camera equipped with CMY sensors, as opposed to RGB sensors (CMY cameras are in fact available). (a) Draw spectral curves roughly depicting what such a camera's sensitivity to wavelength might look like. (b) Could the output of a CMY camera be used to produce ordinary RGB pictures? How?

Suppose a square image has $N^{2}$ pixels. We would like to approximately know how many pixels there are in total in a $(P+1)$ -level image pyramid consisting of the original image plus $P$ smaller images, each of which is $1 / 4$ the size. As a first approximation, let's just count all possible levels, down to a size 1x1 image. (a) First, suppose $N$ is a power of 2 . What is an expression for the exact count of pixels in this case, if $N=2^{M}$ ? What is the exact count of pixels in this case, if $N=16$ ? Write the total as a binary and as a decimal number. (b) Suppose $N$ is not a power of 2 . Just give an upper bound for the number of pixels, assuming there are an infinite number of pyramid levels and we can use floats for numbers of pixels. What is this upper bound if $N=16$ ? Hint: for $x<1$ the Taylor series expansion of $1 /(1-x)$ is $1+x+x^{2}+x^{3}+\ldots$ . What does this mean if $x=1 / 4$ ?

Another name for zig-zag coding is "zonal coding". Suppose you invent a new zonal coding scheme for JPEG that simply discards anti-diagonals above the first few - i.e., we discard the higher frequency ones. Suppose we keep the first six zig-zag lines. (a) How many coefficients are we keeping? (b) How will we do, compared to keeping all the zig-zags (still using run-length encoding). Comment on both compression capability and image quality.

Write down an algorithm (pseudocode) for defining and calculating a colour histogram for RGB data.

How does ATM support multimedia transmission, in particular QoS requests?

Compare and contrast the (a) bandwidth (i.e., bitrate), and (b) playback requirements of uncompressed digital audio and video.

The "hue" is the colour, independent of brightness and how much pure white has been added to it. We can make a simple definition of hue as the set of ratios R:G:B. Suppose a colour (i.e., an RGB) is divided by 2.0, so that the RGB triple now has values 0.5 times its former values. Explain using numerical values: (a) If gamma-correction is not applied, does the second RGB have the same hue as the first RGB, when displayed? (we're not discussing any psychophyisical effects that change our perception - here we're just worried about the machine itself). (b) State all colour triples for which the hue is unchanged.

Suppose you wish to transmit a stereo audio signal through a 1 mega-bit/s connection in real time. Consider the following scenarios: i) You are using a sampling frequency of $44.1 \mathrm{kHz}$ . What is the maximum average number of bits can you use to represent an audio sample? ii) You want to use $16 \mathrm{bit} / \mathrm{sample} / \mathrm{channel}$ representation. What is the maximum sampling frequency? What will you need to do in order to avoid aliasing? iii) You want to use a sampling frequency of $44.1 \mathrm{KHz}$ , and also want use $16 \mathrm{bit} / \mathrm{sample} / \mathrm{channel}$ representation. What is the minimum compression ratio you need in order to transmit the audio signal?

Suppose we acquire a video which has been compressed using Motion-JPEG, and import it into Adobe Premiere (or a similar program). Then we create a movie using an MPEG-4 codec. Comment on the (a) compression ratio (b) appearance of the resulting video.

Please define "motion estimation". (b) Please define "motion compensation".

State Shannon-Fano Algorithm. (b) Complete the following table using the Shannon-Fano Algorithm 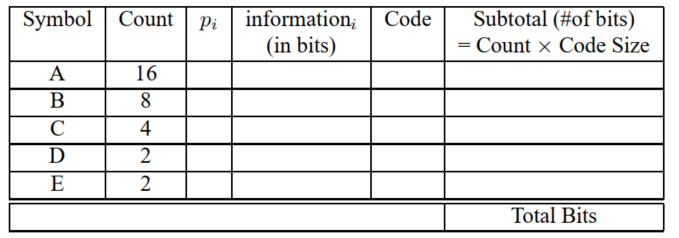(c) What is the entropy of this source, and in what units? Compare to the above result.

When we create a sprite, we usually completely replace pixel values by those in the sprite. Suppose, however, we wish to replace pixel values by a combination with weights $\alpha$ from the original background, plus $(\alpha-1)$ from the sprite, where $\alpha$ is in $[0,1]$ . State how you could do this, using only LOGICAL operators and an ADD. For this question, assume the following: (1) You already have a sprite $S_{\alpha}$ which has the character's colors all multiplied by the factor $\alpha$ , and black outside the character; (2) You already have a second image of the (entire) background, already multiplied by $(1-\alpha)$ , called $B_{1-\alpha}$ . Answer:

In JPEG, each nonzero AC coefficient is described by a composite 8-bit value I='nnnnssss', where 'nnnn' codes the runlength and 'ssss' codes the category. Every DCT coefficient has a category $k$ , where values are in the range $\left[2^{k-1}, 2^{k}-1\right]$ or $\left[-2^{k}+1,-2^{k-1}\right]$ , with $1 \leq k \leq 10$ for the baseline system. For category $k$ , it is necessary to send $k$ bits to specify the sign and the magnitude of the actual DCT coefficient itself. The 4 bits 'nnnn' give the position of the current coefficient relative to the previous nonzero coefficient, i.e., the runlength of zero coefficients from the previous nonzero coefficient. The runlengths specified by 'nnnn' may range from 0 to 15 , and a separate symbol, $I=' 11110000$ ' $=240$ represents a runlength of 16 zero coefficients. If the runlength $>16$ zero coefficients, it is coded by using multiple symbols. A special symbol, $\mathrm{I}=0$ , is used to code the end of block (EOB), signaling all remaining coefficients in the block are zero. The composite symbols for each block are then Huffman coded, followed by additional bits for the sign and magnitude of the actual DCT coefficient itself. Question: How many elements are there in the total symbol set for Huffman coding, encompassing categories, runlengths, and additional symbols? (we're not concerned with the sign and magnitude bits, here.)

Draw a curve showing the relationship of the CIELAB brightness axis to the luminance Y. (b) What curve studied elsewhere in this course does this resemble? Why is that the case?

In many Computer Graphics applications, $\gamma$ -correction is performed only in a color LUT (look-up table). Give pseudocode for how to make such a lookup table, for an 8-bit CLUT, if it is meant for use in $\gamma$ -correction. Show the first 5 entries of the color LUT.

In MIDI, for Channel Messages, how many different "opcodes" can there be in the Status Byte? Why?

Generally, for gray input images what are half-toning and dithering? How are they related to each other? What is ordered dithering?

Suppose we view a decompressed 512×512 JPEG image, but use only the colour part of the stored image information, not the luminance part, to decompress. What does the $512 \times 512$ colour image look like? Assume JPEG is compressed using a 4:2:0 scheme.

In many Computer Graphics applications, $\gamma$ - correction is performed only in a color LUT (look-up table). Show the first 5 entries of the color LUT if it is meant for use in $\gamma$ -correction.

Consider a block (8x8 pixels) of an image as shown below. In a particular color plane, the pixel values are as follows: 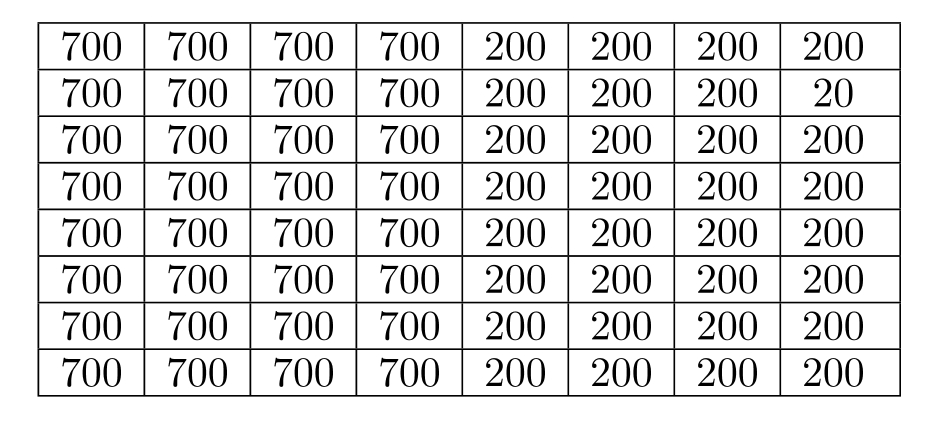A standard 2-D DCT for an $8 \times 8$ block size is defined as $F(u, v)=\frac{C(u) C(v)}{4} \sum_{i=0}^{7} \sum_{j=0}^{7} \cos \frac{(2 i+1) \cdot u \pi}{16} \cos \frac{(2 j+1) \cdot v \pi}{16} f(i, j),$ where $i, j, u, v$ are in $0 . .7$ , and the constants $C(u)$ and $C(v)$ are determined by $C(\xi)=\left\{\begin{array}{cl}\frac{\sqrt{2}}{2} & \text { if } \xi=0 \\1 & \text { otherwise. }\end{array}\right.$ Suppose we compute a DCT $F(u, v)$ , where $u$ is rows and $v$ is columns. (a) What value does $F(0,0)$ have? Explain. (b) Describe the contents (roughly) of the other components. Explain. Hint: Just thinking about it, rather than calculating everything, will save you time. What are values $F(u, 0)$ . What are values $F(0, v)$ . What are other values $F(u, v)$ .