Exam 5: Growth and Decay: An Introduction to Exponential Functions

The half-life of Beryllium 11 is 13.81 seconds. If a sample initially contains 2,800 atoms, create a formula to represent the number of atoms, A, in the sample after T intervals of 13.81 seconds.

A company states that their annual profit has increased by 695% over the last 12 years from 1998 to 2010. Write a function to describe the profit with f(0) being 1998 profits of $186700. Round the growth factor to 3 decimal places if necessary.

Create the formula for the graph.

Find an exponential function with initial value 30 and decay rate 0.1. Write your answer in 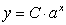form.

An outbreak of a flu virus begins with 6 people infected and the number of people infected increases by a factor of 4.2 each week. Find a formula that gives the number of people infected, I, as a function of the weeks, w, since the outbreak began.

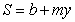A new cell phone company has 600 subscribers their first year (year 0) and their business grows to 1,000 subscribers the next year (year 1). Find a formula for the number of subscribers, C, as a function of the years in business, y, assuming… A) linear growth (write your answer in the form ) , and B) exponential growth (write your answer in the form 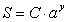)Now use these functions to predict how many subscribers they will have in their 20th year of business (year 19) assuming... C) linear growth and D) exponential growth.Round values to 2 decimal places.

The following function gives the amount, A, of a radioactive element remaining as a function of y, the years of decay: 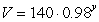Find the half-life to the nearest year.

Find the growth factor (assuming exponential growth) for a population that grows from 1,100,000 to 1,716,000 in one year.

When an event happens in a community, news travels fast. Assuming 4 people initially know the news and the number of people who hear the news increases by a factor of 4.3 each hour, find a formula that gives the number of people who hear the news, N, as a function of the hours, h, since the event happened.

A quantity, Q, doubles every 5 years. Write a formula for the quantity of Q where T = the number of 5 year periods and the amount of the original substance is 580 grams.

Determine whether the data is linear or exponential.

The following function gives the value, V, of an investment as a function of y, the years since the original investment: 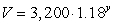Use the "Rule of 70" to estimate the doubling time to the nearest year.

Write a function in the form 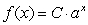for an exponential function where 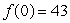and for every unit increase in x, the output is multiplied by 0.3.

Alice invests $18,000 in an account offering 3% interest compounded biannually (2 times per year). A) Find the value of the account after 8 years. Round your answer to the nearest cent. B) How many years until the account value reaches $34,000? Round your answer to the nearest year.

A house valued at $45,000 in 1989 increased in value to $140,000 in 2001 Choose the true statement.

Find A) the continuous growth factor and B) the effective growth factor from the function, 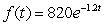Write your answers as percents rounded to 2 decimal places, like 23.75%.

A house valued at $45,000 in 1990 increased in value to $100,000 in 2005. A) Find a function which gives the value of the house, V, as a function of y, the number of years after 1990. Write your answer in 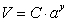form and round values to 2 decimal places. B) Now use that function to predict the value of the house in 2018.Round to 2 decimal places.

The price of a new car increases by 21% every 5 years. What is the annual percent increase? Round to the nearest hundredth of a percent.

How many years does it take for this function to double?

A house valued at $65,000 in 1989 increased in value to $105,000 in 2004 A) What was the absolute change in value? B) What was the percent change over the 15 years? Round to 2 decimal places, if necessary.