Exam 4: Game Theory: Games Between Three or More Players

Figure 4.1 : 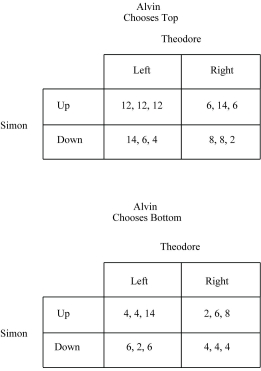-Refer to Figure 4.1. The game described in the payoff matrix has the characteristics of a(n) ________ game.

In a multiplayer game where there are two equally-enjoyable choices of what to do, and everyone wants to do what everyone else is doing, there will be three Nash equilibria.

In n-player games, any number of players between 4 and infinity can theoretically play.

Figure 4.3: 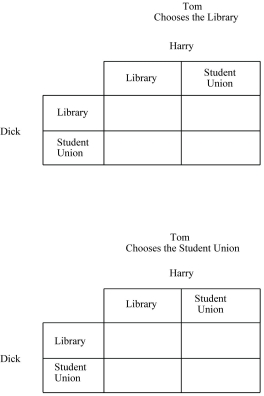-Refer to Figure 4.3. Tom, Dick, and Harry all want to meet up at either at the Library or the Student Union, but none knows with certainty where the other two will go. They will consider their mission a success if all three meet at the same location, but will consider their mission a failure if all three do not meet at the same location. Fill in the above payoff matrix, assigning a payoff of 1 for each player when their mission is a success and a payoff of 0 for each player when their mission is a failure. Do any of the three players have a dominant strategy? If yes, identify the strategy. Are there any Nash equilibria that exist? If yes, identify them.

Figure 4.1 : -Refer to Figure 4.1. Simon's available strategies include

Figure 4.7: 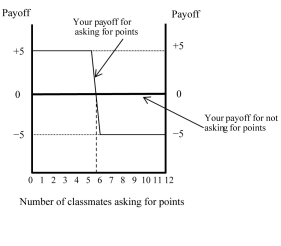Your economics professor offers you the opportunity to ask for extra points on your midterm exam. All you have to do is write "please give me points" at the bottom of the last page of the exam. Depending on the number of students who choose to ask for the extra points, either 5 points will be added to those students' grades, or 5 points will be deducted from those students' grades. If you write nothing, your grade will stay the same. There are 12 students, including you, in the class. The payoffs for this game are shown in the above figure. -Refer to Figure 4.7. An equilibrium occurs when how many students ask for points?

What is an "n-player game"? What doe the "n"represent"?

Figure 4.2: -Refer to Figure 4.2. The game described in the payoff matrix is an example of a(n) ________ game.

Figure 4.1 : -Refer to Figure 4.1. Theodore is the ________ player.

Figure 4.1 : -Refer to Figure 4.1. Suppose Alvin chooses Bottom, while Simon chooses Up, and Theodore chooses Right. Alvin's payoff will be

Figure 4.1 : -Refer to Figure 4.1. The dominant strategy for Simon is

In a three-player game, which of the following is not one of the player designations for a payoff matrix?

Figure 4.2: -Refer to Figure 4.2. Use best-response analysis to answer the following question. If Ferris's choice placed us in the movie theater, Sloane's best response, depending on the column she finds herself in, would include choosing all of the following cells except the one located at the ________ section of the appropriate payoff matrix.

Economists often refer to games with more than three players as

Figure 4.8: You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure. -Refer to Figure 4.8. If half of your friends go to the beach and half go to the park, you will receive a payoff of ________ if you go to the park.

Figure 4.8: You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure. -Refer to Figure 4.8. How many stable Nash equilibrium points are there in this game?

Figure 4.2: -Refer to Figure 4.2. The dominant strategy for Cameron is to

Figure 4.2: -Refer to Figure 4.2. How many Nash equilibria exist in this game?

Figure 4.1 : -Refer to Figure 4.1. Alvin is the ________ player.

Figure 4.8: You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure. -Refer to Figure 4.8. How many different Nash equilibrium points are there in this game?