Exam 7: Advanced Regression Analysis
Exam 1: Introduction to Business Analytics44 Questions
Exam 2: Data Management and Wrangling46 Questions
Exam 3: Data Visualization and Summary Measures52 Questions
Exam 4: Probability and Probability Distributions50 Questions
Exam 5: Statistical Inference53 Questions
Exam 6: Regression Analysis53 Questions
Exam 7: Advanced Regression Analysis52 Questions
Exam 8: Introduction to Data Mining54 Questions
Exam 9: Supervised Data Mining: K-Nearest Neighbors and Naãve Bayes54 Questions
Exam 10: Supervised Data Mining: Decision Trees51 Questions
Exam 11: Unsupervised Data Mining53 Questions
Exam 12: Forecasting With Time Series Data53 Questions
Exam 13: Introduction to Prescriptive Analytics49 Questions
Select questions type
What is the predicted value ( ) when the numerical variable is x = 70 for the regression equation = ?831 + 29.0x ? 0.113x2?
Free
(Multiple Choice)
4.8/5  (36)
(36)
Correct Answer:
C
Consider a linear regression model where y represents the response variable and d1 and d2 represent two dummy variables. The model is estimated as = -2.49 + 1.86x + 3.20d1 - 2.21d2 + 0.50d1d2. Compute for x = 3, d1 = 1, and d2 = 0.
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
D
Using a sample of 50, the following regression output is obtained from estimating the linear probability regression model y = 0 + 1x + . What is the predicted probability when x = 14? 
Free
(Multiple Choice)
4.8/5  (40)
(40)
Correct Answer:
B
In the k-fold cross-validation method, the smaller the k value, the greater the reliability of the k-fold method.
(True/False)
5.0/5  (40)
(40)
Consider a binary response variable y and a predictor variable x that varies between 0 and 5. The linear model is estimated as 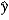 = -2.90 + 0.65x. What is the estimated probability for x = 5?
= -2.90 + 0.65x. What is the estimated probability for x = 5?
(Multiple Choice)
4.9/5  (39)
(39)
The following table contains the parameter estimates of the linear probability regression model and the logistic regression model. When considering a binary response variable y and two predictor variables, x1 and x2, What is the estimated linear probability implied by the logistic probability regression model for x1 = 3 with x2 = 9? 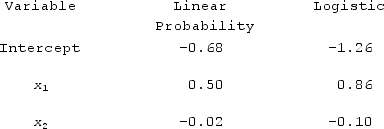
(Multiple Choice)
4.9/5  (41)
(41)
Which interpretation of a linear probability regression model represents the estimate ^P = -40 + 0.05x?
(Multiple Choice)
4.8/5  (43)
(43)
In the following logarithmic regression model, 1 × 0.01 measures the approximate unit change in E(y) when x increases. If 1 = 6,000, then what is the unit change in E(y)?
(Multiple Choice)
4.8/5  (44)
(44)
In determining the partial effect on dummy variable d in a regression model with an interaction variable = b0 + b1x + b2d + b3xd, the numeric variable x value needs to be known.
(True/False)
5.0/5  (42)
(42)
Christian Za is using the holdout method to partition his data into two independent and mutually exclusive sets: 75% in a training set and 25% in a validation set. Based on an R2 value of 0.4532 and RMSE of 0.3268 for the training set and an R2 value of 0.1426 and RMSE of 0.5371 for the validation set, which of the competing models is the preferred model?
(Multiple Choice)
4.8/5  (42)
(42)
Consider a linear regression model where y represents the response variable and d1 and d2 represent two dummy variables. The model is estimated as = -2.53 + 2.04x + 4.20d1 - 2.86d2 + 0.68d1d2. Compute for x = 3, d1 = 1, and d2 = 0.
(Multiple Choice)
4.9/5  (43)
(43)
Because software packages use random draws of the observations to partition data, the results will not be identical to a fixed partitioning of the observations.
(True/False)
4.9/5  (32)
(32)
In using both the linear probability regression and the logistic regression models for n = 40, the following table is the analysis of the holdout method. Based on the table, what is the impact of changing the to binary predictions? 
(Multiple Choice)
4.9/5  (36)
(36)
ln(y) = 0 + 1 ln(x) + represents the exponential regression model.
(True/False)
4.7/5  (46)
(46)
In the linear probability regression model, the response variable y will equal 1 or 0 to represent the probability of success.
(True/False)
4.7/5  (44)
(44)
Sam, a marketing manager for XYZ big box stores, is trying to determine if there is a relationship between shelf space (in feet) and sales (in hundreds of dollars). To do this, Sam selected the top 12 producing locations. Using the provided Model 1 results, which option best interprets the impact of the coefficients and p-values?
 * the p-value
* the p-value
(Multiple Choice)
4.8/5  (48)
(48)
The estimate regression equation for the average cost of widgets is:
^Widgets = 7.23 - 0.2478 Output + 0.1954 Output2. Both predictor variables are statistically significant at 5% level, confirming the quadratic effect. What is the predictive average from an output level of 2 million units to 3 million units?
(Multiple Choice)
4.7/5  (34)
(34)
The estimate regression equation for the average cost of widgets is:
^Widgets = 7.33 - 0.2340 Output + 0.1892 Output2. Both predictor variables are statistically significant at 5% level, confirming the quadratic effect. What is the predictive average from an output level of 2 million units to 3 million units?
(Multiple Choice)
4.8/5  (35)
(35)
Consider the sample correlation coefficients in the table below. How much of the variability in time can be explained by boxes using the alternative way of to determine the coefficient of determination. 
(Multiple Choice)
4.8/5  (35)
(35)
To test for the accuracy rate in a binary choice model, the number of correct classification observations for both outcomes should be reported.
(True/False)
4.9/5  (36)
(36)
Showing 1 - 20 of 52
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)