Exam 6: Radical Expressions, Equations and Functions
Exam 1: Fundamentals of Algebra120 Questions
Exam 2: Polynomials and Absolute Value52 Questions
Exam 3: Relations and Functions92 Questions
Exam 4: Systems of Linear Equations90 Questions
Exam 5: Rational Expressions, Equations and Functions121 Questions
Exam 6: Radical Expressions, Equations and Functions71 Questions
Exam 7: Quadratic Expressions, Equations and Functions105 Questions
Exam 8: Exponential and Logarithmic Expressions, Equations and Functions48 Questions
Exam 9: Conic Sections Systems of Non-Linear Equations73 Questions
Exam 10: Sequences, Series and the Binomial Theorem60 Questions
Select questions type
Write the radical expression as an exponential expression and simplify. 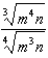
(Multiple Choice)
4.7/5  (44)
(44)
Simplify the expression. Assume that all factors of the radicand are nonnegative. 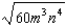
(Multiple Choice)
4.8/5  (37)
(37)
Simplify. Assume that all factors of the radicand are nonnegative. 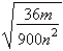
(Multiple Choice)
4.9/5  (40)
(40)
The time T (in seconds) required for a pendulum to make one complete swing back and forth is approximated by the formula 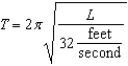 , where L is the length of the pendulum. T is called the period of the pendulum. Use
, where L is the length of the pendulum. T is called the period of the pendulum. Use 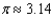 To find the length in feet of a pendulum with a period of 6 seconds. Round your answer to the nearest foot.
To find the length in feet of a pendulum with a period of 6 seconds. Round your answer to the nearest foot.
(Multiple Choice)
4.9/5  (38)
(38)
Showing 21 - 40 of 71
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)