Exam 10: Sequences, Series and the Binomial Theorem
Exam 1: Fundamentals of Algebra120 Questions
Exam 2: Polynomials and Absolute Value52 Questions
Exam 3: Relations and Functions92 Questions
Exam 4: Systems of Linear Equations90 Questions
Exam 5: Rational Expressions, Equations and Functions121 Questions
Exam 6: Radical Expressions, Equations and Functions71 Questions
Exam 7: Quadratic Expressions, Equations and Functions105 Questions
Exam 8: Exponential and Logarithmic Expressions, Equations and Functions48 Questions
Exam 9: Conic Sections Systems of Non-Linear Equations73 Questions
Exam 10: Sequences, Series and the Binomial Theorem60 Questions
Select questions type
For all the problems in this set the domain is the set of positive integers greater than 0.
Find a formula for the nth term of each sequence.
-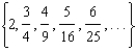
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
C
For all the problems in this set the domain is the set of positive integers greater than 0.
-Use sigma notation to represent the partial sum of the first eight terms of the sequence 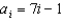
Free
(Multiple Choice)
4.9/5  (30)
(30)
Correct Answer:
D
For all the problems in this set the domain is the set of positive integers greater than 0.
-Use sigma notation to represent the partial sum of the first twelve terms of the sequence 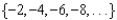
Free
(Multiple Choice)
4.9/5  (30)
(30)
Correct Answer:
C
Do not use Pascal's Triangle.
-Find the coefficient of the 9th term in the binomial expansion of 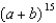
(Multiple Choice)
4.9/5  (27)
(27)
For all the problems in this set the domain is the set of positive integers greater than 0.
-Evaluate the partial sum 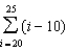
(Multiple Choice)
4.9/5  (36)
(36)
Use Pascal's Triangle and the binomial theorem to find the 8th term in the expansion of 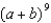
(Multiple Choice)
4.8/5  (40)
(40)
Expand the expression. Use Pascal's Triangle to find the coefficients and use the binomial theorem to find the variables in each term.
-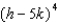
(Multiple Choice)
5.0/5  (33)
(33)
Expand the expression. Use Pascal's Triangle to find the coefficients and use the binomial theorem to find the variables in each term.
-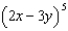
(Multiple Choice)
4.8/5  (37)
(37)
For all the problems in this set the domain is the set of positive integers greater than 0.
-Evaluate the partial sum of the first four terms of the sequence 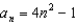
(Multiple Choice)
4.8/5  (46)
(46)
Find the common ratio, r, of the given geometric sequence.
-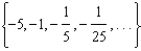
(Multiple Choice)
4.8/5  (39)
(39)
For all the problems in this set the domain is the set of positive integers greater than 0.
Use roster notation to represent the range of the sequence.
-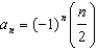
(Multiple Choice)
4.7/5  (39)
(39)
The tenth term in a geometric sequence is 1,000,000,000. The common ratio is 10.
-Find the 11th term of the sequence.
(Multiple Choice)
4.8/5  (33)
(33)
For all the problems in this set the domain is the set of positive integers.
Find a formula for the nth term of the arithmetic sequence.
-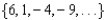
(Multiple Choice)
4.9/5  (41)
(41)
Use Pascal's Triangle and the binomial theorem to find the 3rd term in the expansion of 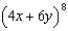
(Multiple Choice)
4.9/5  (32)
(32)
Expand the expression. Use Pascal's Triangle to find the coefficients and use the binomial theorem to find the variables in each term.
-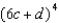
(Multiple Choice)
4.8/5  (36)
(36)
The expression 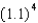 is equivalent to
is equivalent to 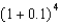 . Expand this expression using Pascal's Triangle and the binomial theorem to find the sum of the terms.
. Expand this expression using Pascal's Triangle and the binomial theorem to find the sum of the terms.
(Multiple Choice)
4.7/5  (44)
(44)
For all the problems in this set the domain is the set of positive integers.
Find a formula for the nth term of the arithmetic sequence.
-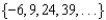
(Multiple Choice)
5.0/5  (36)
(36)
Find the common ratio, r, of the given geometric sequence.
-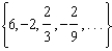
(Multiple Choice)
4.8/5  (38)
(38)
For all the problems in this set the domain is the set of positive integers.
-The first row in an auditorium has 10 seats. Each successive row has 4 more seats. Use a partial sum to find the total number of seats in the first 20 rows.
(Multiple Choice)
4.9/5  (35)
(35)
Showing 1 - 20 of 60
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)