Exam 12: Risk Analysis
Exam 1: The Nature and Scope of Managerial Economics, Optimization Techniques and New Management Tools23 Questions
Exam 2: Demand Theory26 Questions
Exam 3: Demand Estimation12 Questions
Exam 4: Demand Forecasting18 Questions
Exam 5: Production Theory and Estimation42 Questions
Exam 6: Cost Theory and Estimation31 Questions
Exam 7: Market Structure: Perfect Competition, Monopoly, and Monopolistic Competition36 Questions
Exam 8: Oligopoly and Firm Architecture21 Questions
Exam 9: Game Theory and Strategic Behavior23 Questions
Exam 10: Pricing Practices13 Questions
Exam 11: Regulation and Antitrust: The Role of Government in the Economy15 Questions
Exam 12: Risk Analysis17 Questions
Exam 13: Long-Run Investment Decisions: Capital Budgeting10 Questions
Select questions type
When there is only one possible outcome to a decision, risk or uncertainty is present.
Free
(True/False)
4.9/5  (35)
(35)
Correct Answer:
False
A firm is considering three business projects. Project A will return a profit of $1 if conditions are poor, $7 if conditions are good, and $8 if conditions are excellent. Project B will return a profit of $1 if conditions are poor, $4 if conditions are good, and $11 if conditions are excellent. Project C will return a profit of $8 if conditions are poor, $3 if conditions are good, and $5 if conditions are excellent.
(i) Use the maximin criterion to determine the preferred project. Show how you arrived at your solution.
(ii) Calculate the regret matrix.
(iii) Use the minimax regret criterion to determine the preferred project. Show how you arrived at your solution.
Free
(Essay)
4.9/5  (28)
(28)
Correct Answer:
(i) The minimum profit for A is $1, for B is $1, and for C is $3. The maximin solution ($3) is Project C.
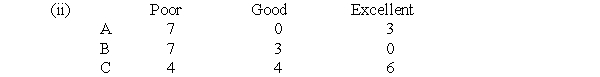 (iii) The maximum regret for A is $7, for B is $7, and for C is $6. The minimax regret solution ($6) is Project C.
(iii) The maximum regret for A is $7, for B is $7, and for C is $6. The minimax regret solution ($6) is Project C.
The maximin criterion is a method of dealing with uncertainty.
Free
(True/False)
4.9/5  (38)
(38)
Correct Answer:
True
A firm is considering three business projects. Project A will return a profit of $5 if conditions are poor, $10 if conditions are good, and $15 if conditions are excellent. Project B will return a profit of $12 if conditions are poor, $8 if conditions are good, and $4 if conditions are excellent. Project C will return a profit of $3 if conditions are poor, $20 if conditions are good, and $7 if conditions are excellent.
(i) Use the maximin criterion to determine the preferred project. Show how you arrived at your solution.
(ii) Calculate the regret matrix.
(iii) Use the minimax regret criterion to determine the preferred project. Show how you arrived at your solution.
(Essay)
4.9/5  (35)
(35)
The Z value for a particular outcome is equal to the difference between the outcome and the expected outcome measured in terms of standard deviations.
(True/False)
4.9/5  (35)
(35)
Investment A has an expected value of 5 and a standard deviation of 2. Investment B has an expected value of 10 and a standard deviation of 5. Using the coefficient of variation approach to comparing these two investments,
(Multiple Choice)
4.9/5  (35)
(35)
A firm is considering three business projects. Project A will return a loss of $5 if conditions are poor, a profit of $4 if conditions are good, and a profit of $8 if conditions are excellent. Project B will return a profit of zero if conditions are poor, a profit of $2 if conditions are good, and a profit of $7 if conditions are excellent. Project C will return a profit of $1 if conditions are poor, $3 if conditions are good, and $5 if conditions are excellent.
(i) Use the maximin criterion to determine the preferred project. Show how you arrived at your solution.
(ii) Calculate the regret matrix.
(iii) Use the minimax regret criterion to determine the preferred project. Show how you arrived at your solution.
(Essay)
4.8/5  (41)
(41)
A firm is considering three business projects. Project A will return a profit of $1 if conditions are poor, $5 if conditions are good, and $8 if conditions are excellent. Project B will return a profit of $2 if conditions are poor, $2 if conditions are good, and $6 if conditions are excellent. Project C will return a profit of $10 if conditions are poor, $1 if conditions are good, and $2 if conditions are excellent.
(i) Use the maximin criterion to determine the preferred project. Show how you arrived at your solution.
(ii) Calculate the regret matrix.
(iii) Use the minimax regret criterion to determine the preferred project. Show how you arrived at your solution.
(Essay)
4.9/5  (42)
(42)
A firm is considering two business projects. Project A will return a loss of $45 if conditions are poor, a profit of $35 if conditions are good, and a profit of $155 if conditions are excellent. Project B will return a loss of $100 if conditions are poor, a profit of $60 if conditions are good, and a profit of $300 if conditions are excellent. The probability distribution of conditions follows:
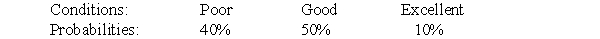 (i) Calculate the expected value of each project and identify the preferred project according to this criterion.
(ii) Calculate the standard deviation of each project and identify the project that has the higher level of risk.
(iii) Calculate the coefficient of variation for each project and identify the preferred project according to this criterion.
(i) Calculate the expected value of each project and identify the preferred project according to this criterion.
(ii) Calculate the standard deviation of each project and identify the project that has the higher level of risk.
(iii) Calculate the coefficient of variation for each project and identify the preferred project according to this criterion.
(Essay)
4.7/5  (35)
(35)
Branches coming out of circles on decision trees show alternative courses of action that can be selected by decision makers.
(True/False)
4.8/5  (43)
(43)
A firm is considering two business projects. Project A will return a profit of zero if conditions are poor, a profit of $4 if conditions are good, and a profit of $8 if conditions are excellent. Project B will return a profit of $2 if conditions are poor, a profit of $3 if conditions are good, and a profit of $4 if conditions are excellent. The probability distribution of conditions follows:
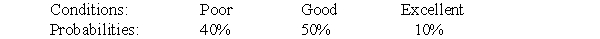 (i) Calculate the expected value of each project and identify the preferred project according to this criterion.
(ii) Assume that the firm has determined that its utility function for profit is as follows:
U(X) = X - 0.05X2
Calculate the expected utility of each project and identify the preferred project according to this criterion.
(iii) Is the firm risk averse, risk neutral, or risk seeking? How can you tell?
(i) Calculate the expected value of each project and identify the preferred project according to this criterion.
(ii) Assume that the firm has determined that its utility function for profit is as follows:
U(X) = X - 0.05X2
Calculate the expected utility of each project and identify the preferred project according to this criterion.
(iii) Is the firm risk averse, risk neutral, or risk seeking? How can you tell?
(Essay)
4.9/5  (50)
(50)
Risk refers to a situation in which the probability of each possible outcome to a decision is unknown or meaningless.
(True/False)
4.9/5  (42)
(42)
A certainty equivalent coefficient of one is used if the decision maker is risk neutral.
(True/False)
4.8/5  (44)
(44)
A firm is considering two business projects. Project A will return a loss of $5 if conditions are poor, a profit of $35 if conditions are good, and a profit of $95 if conditions are excellent. Project B will return a loss of $15 if conditions are poor, a profit of $45 if conditions are good, and a profit of $135 if conditions are excellent. The probability distribution of conditions follows:
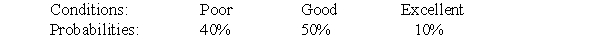 (i) Calculate the expected value of each project and identify the preferred project according to this criterion.
(ii) Calculate the standard deviation of each project and identify the project that has the higher level of risk.
(iii) Calculate the coefficient of variation for each project and identify the preferred project according to this criterion.
(i) Calculate the expected value of each project and identify the preferred project according to this criterion.
(ii) Calculate the standard deviation of each project and identify the project that has the higher level of risk.
(iii) Calculate the coefficient of variation for each project and identify the preferred project according to this criterion.
(Essay)
4.9/5  (42)
(42)
A firm is considering two business projects. Project A will return a profit of zero if conditions are poor, a profit of $16 if conditions are good, and a profit of $49 if conditions are excellent. Project B will return a profit of $4 if conditions are poor, a profit of $9 if conditions are good, and a profit of $49 if conditions are excellent. The probability distribution of conditions follows:
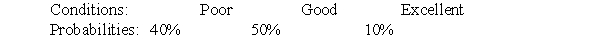 (i) Calculate the expected value of each project and identify the preferred project according to this criterion.
(ii) Assume that the firm has determined that its utility function for profit is equal to the square root of profit. Calculate the expected utility of each project and identify the preferred project according to this criterion.
(iii) Is the firm risk averse, risk neutral, or risk seeking? How can you tell?
(i) Calculate the expected value of each project and identify the preferred project according to this criterion.
(ii) Assume that the firm has determined that its utility function for profit is equal to the square root of profit. Calculate the expected utility of each project and identify the preferred project according to this criterion.
(iii) Is the firm risk averse, risk neutral, or risk seeking? How can you tell?
(Essay)
4.9/5  (33)
(33)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)