Exam 3: Demand Estimation

If the t ratio for the slope of a simple coefficient of a simple linear regression equation is -2.48 and the critical values of the t distribution at the 1% and 5% levels, respectively, are 3.499 and 2.365, then the slope is

Ordinary least squares is used to estimate a linear relationship between a firm's quantity sold per month and its total promotional expenditures, and the slope of the linear function is found to be positive and significantly different from zero. Assuming that all other variables, including product price, were constant during the period covered by the data set, this result implies that

The Drag Net Fishing Company (DNF) has hired you as a consultant to analyze the demand by local restaurants for fresh fish. The available data set includes monthly observations collected over the past five years on the number of hundreds of pounds of fish purchased by local restaurants per month (Q), the price per pound of fish (P), the average cost of a meal at a local restaurant (M), a seasonal variable (S) that is equal to one during the tourist season and zero otherwise, and average household income (in $1,000) in the area. The results of a regression analysis (with standard errors in parenthesis) are given below. (i) Evaluate the statistical significance of the equation as a whole and of each of its coefficients. (ii) The average values of independent variables in the data set that was used to estimate the equation are P = $8, M = $14, and I = $40,000. Calculate a point estimate of the restaurant demand for fish and a 95% interval estimate when it is tourist season. Also, calculate a point estimate of the restaurant demand for fish and a 95% interval estimate when it is not tourist season.

If the observed values of the dependent and independent variables are transformed into their natural logarithms, then each estimated slope coefficient is equal to the elasticity of the dependent variable with respect to the corresponding independent variable.

The log-linear demand function for Beckler's Frozen Pizzas is: lnQ_X = 4 - 3.80 ln P_X + 0.30 ln P_Y + 0.15 ln S + ln A + 1.50 ln I The number of pizzas sold per week (Q_X) depends on the price charged for a pizza (P_X), the price charged for a competitor's brand of pizza (P_Y), the percentage of single parent families (S), monthly advertising expenditures (A) in thousands, and average annual household income (I) in thousands. (i) If P_X = $4.00, P_Y = $3.50, S = 40%, A = $5,000, and I = $40,000, how many pizzas can Beckler's expect to sell in a week? (ii) Interpret the price elasticity, cross-price elasticity, family structure elasticity, advertising elasticity, and income elasticity of demand for pizzas. (iii) The president of Beckler's plans to increase the price of their pizzas by 25% and to increase advertising expenditures by 10%. By what percentage can the number of pizzas sold by Beckler's be expected to change? Will total revenue increase, decrease, or remain the same? Explain your answer. (iv) If Beckler's lowers the price of its pizzas by 5% and increases advertising expenditures by 10% while Beckler's competitor lowers the price of its pizza by 20%, what effect will this have on the number of Beckler's pizzas sold per week?

Just The Fax, Inc. (JTF) has hired you as a consultant to analyze the demand for its line of telecommunications devices in 35 different market areas. The available data set includes observations on the number of thousands of units sold by JTF per month (Q_X), the price per unit charged by JTF (P_X), the average unit price of competing brands (P_Z), monthly advertising expenditures by JTF (A), and average gross sales (in $1,000) of businesses in the market area (I). The results of a regression analysis (with standard errors in parenthesis) are given below. 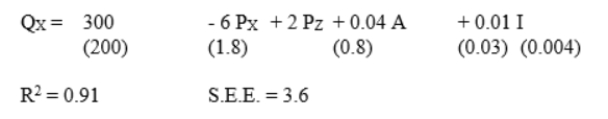(i) Evaluate the statistical significance of the equation as a whole and of each of its coefficients. (ii) The average values of the independent variables in the data set used to estimate the equation are P_X = $195, P_Z = $225, A = $11,000, and I = $200,000. Calculate a point estimate of JTF's average sales and a 95% interval estimate of sales based on these values.

The adjusted value of the coefficient of determination

Ordinary least squares is used to estimate a linear relationship between a firm's total revenue per week (in $1,000s) and the average percentage discount from list price allowed to customers by salespersons. A 95% confidence interval on the slope is calculated from the regression output. The interval ranges from 1.05 to 2.38. Based on this result, the researcher

Florid Technologies is a manufacturer of exercise machines. Their best selling device, a mechanical swimming simulator, has been on the market for several years. The demand function for the simulator was estimated in log-linear form using time-series data. The results are presented below. Q_X = 110 P_X^-0.20 P_Y^0.30 P_Z^-0.10 A^0.10 I^0.01 The number of simulators sold per week (Q_X) was found to depend on the price charged for a simulator (P_X), the average monthly cost of membership at a health club (P_Y), the cost of an accessory package designed for use with the simulator (P_Z), monthly advertising expenditures (A) in thousands, and average annual household income (I) in thousands. (i) If P_X = $595, P_Y = $45, P_Z = $99.85, A = $11,000, and I = $44,000, how many simulators can Florid Industries expect to sell in a week? (ii) Interpret the price elasticity, cross-price elasticities, advertising elasticity, and income elasticity of demand for simulators. (iii) The president of Florid Technologies plans to increase the simulator's price by 10% and to increase advertising expenditures by 5%. By what percentage can sales of simulators be expected to change? Will total revenue increase, decrease, or remain the same? Explain your answer. (iv) If the price of a simulator is increased by 10% and the cost of an accessory package is reduced by 20%, what effect will this have on simulator sales?

regression equation is equal to 3.614 and the critical values of the t distribution at the 1% and 5% levels of significance, respectively, are 3.499 and 2.365, then the slope is

The Durbin-Watson statistic is used to test the significance of the standard error of the regression.

If the t ratio for the slope of a simple linear regression equation is equal to 1.614 and the critical values of the t distribution at the 1% and 5% levels of significance, respectively, are 3.499 and 2.365, then the slope is