Exam 4: Polynomials: Operations
Exam 1: Introduction to Real Numbers and Algebraic Expressions536 Questions
Exam 2: Solving Equations and Inequalities265 Questions
Exam 3: Graphs of Linear Equations192 Questions
Exam 4: Polynomials: Operations392 Questions
Exam 5: Polynomials: Factoring215 Questions
Exam 6: Rational Expressions and Equations204 Questions
Exam 7: Systems of Equations80 Questions
Exam 8: Radical Expressions and Equations154 Questions
Exam 9: Quadratic Equations185 Questions
Exam 10: Equations of Lines and Simplifying Radical Expressions133 Questions
Select questions type
Solve the problem.
-An object's altitude, in meters, is given by the polynomial , where is the height in meters from which the launch occurs, is the initial upward speed in meters per second, and is the number of seconds for which the rocket is airborne. A pebble is shot upward from the top of a building 191 meters tall. If the initial speed is 35 meters per second, how high above the ground will the pebble be after 2 seconds? Round results to the nearest tenth of a meter.
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-Find a polynomial for the perimeter of the figure.
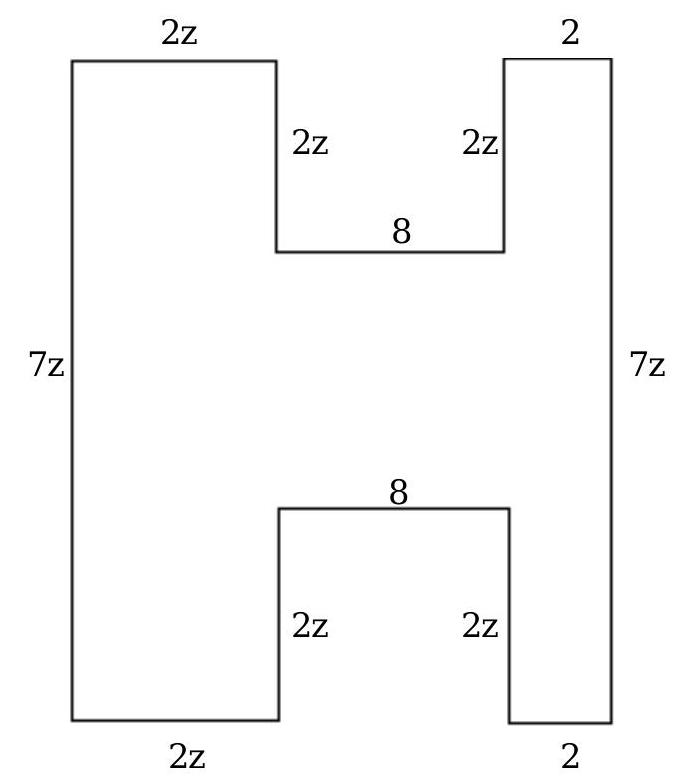
(Multiple Choice)
4.8/5  (43)
(43)
Collect like terms and then arrange in descending order.
-
(Multiple Choice)
4.8/5  (43)
(43)
Solve the problem.
-An oval running track encircles a soccer field that is yards wide and yards long (see figure). The area of the region enclosed by the track can be calculated using the equation . Calculate the area if and . Use the approximation .
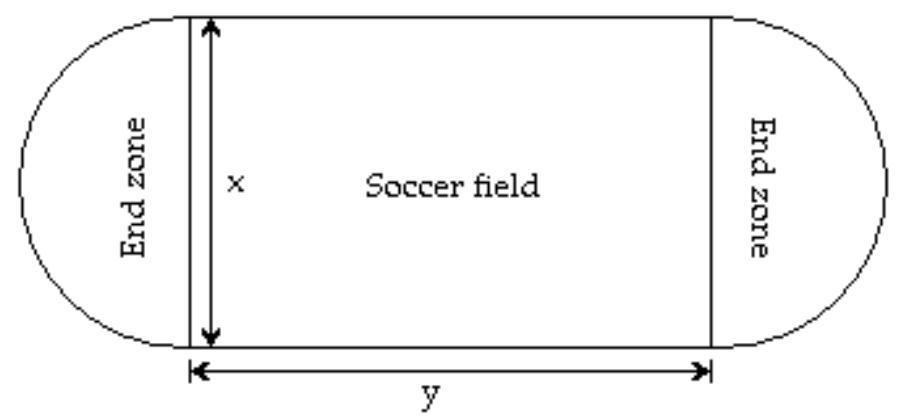
(Multiple Choice)
4.9/5  (36)
(36)
Showing 301 - 320 of 392
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)