Exam 10: Conic Sections
Exam 1: Review of Real Numbers152 Questions
Exam 2: Linear and Absolute Value Equations and Inequalities334 Questions
Exam 3: Graphing Linear Equations353 Questions
Exam 4: Systems of Equations204 Questions
Exam 5: Exponents, Polynomials, and Factoring Polynomials453 Questions
Exam 6: Rational Expressions and Equations249 Questions
Exam 7: Radical Expressions and Equations361 Questions
Exam 8: Quadratic Equations270 Questions
Exam 9: Logarithmic and Exponential Functions404 Questions
Exam 10: Conic Sections122 Questions
Exam 11: Sequences, Series, and the Binomial Theorem154 Questions
Select questions type
Solve the system by the substitution method.
-
Free
(Multiple Choice)
4.8/5  (41)
(41)
Correct Answer:
C
Find the midpoint of the line segment that connects the given points.
- and
Free
(Multiple Choice)
5.0/5  (37)
(37)
Correct Answer:
B
Find the equation of the parabola of the form that passes through the given three points.
-
Free
(Multiple Choice)
4.8/5  (40)
(40)
Correct Answer:
B
Find the center and radius of the circle by completing the square.
-
(Multiple Choice)
4.7/5  (37)
(37)
Graph the hyperbola. Give the coordinates of the center as well as the values of and .
-
(Multiple Choice)
4.8/5  (40)
(40)
Find the center and radius of the circle by completing the square.
-
(Multiple Choice)
4.9/5  (35)
(35)
Find the equation of the circle that has a diameter with the given endpoints.
- and
(Multiple Choice)
4.8/5  (46)
(46)
Find the foci of the ellipse. Round to the nearest tenth if necessary.
-
(Multiple Choice)
4.8/5  (31)
(31)
Most video games need to determine whether two objects touch, such as a character and a wall or a missile and an asteroid; this is known as collision detection. One method for doing this is to find a circle that bounds each object. If the distance between the centers of the two objects is less than or equal to the sum of the two radii of the circles that the objects are bounded by, the two objects are touching. Determine whether Object 1 with radius 112 pixels and center at touches Object 2 with radius 154 pixels and center at .
(True/False)
4.8/5  (36)
(36)
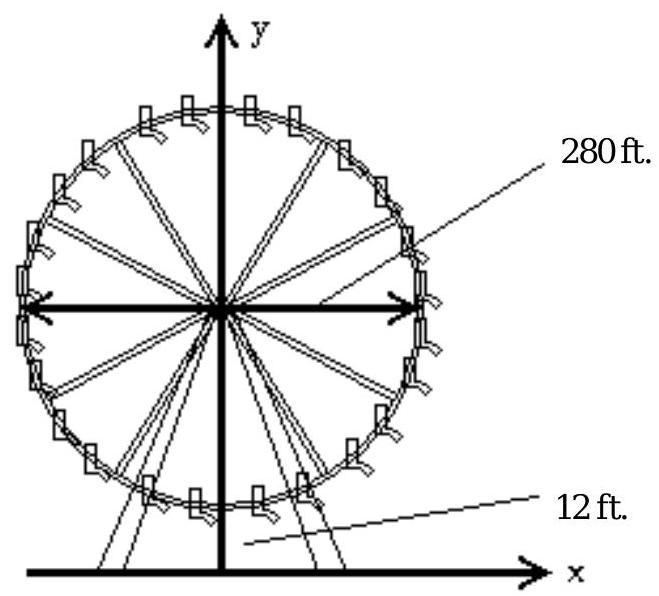
Solve the problem.
-A Ferris wheel has a diameter of 280 feet and the bottom of the Ferris wheel is 12 feet above the ground. Find the equation of the wheel if the origin is placed on the ground directly below the center of the wheel, as illustrated.
(Multiple Choice)
4.9/5  (38)
(38)
Graph the hyperbola. Give the coordinates of the center as well as the values of and .
-
(Multiple Choice)
4.9/5  (27)
(27)
Graph the circle. State the center and radius of the circle
-
(Multiple Choice)
4.8/5  (38)
(38)
Graph the circle. State the center and radius of the circle
-
(Multiple Choice)
4.8/5  (36)
(36)
Find the equation of the parabola of the form that passes through the given three points.
-
(Multiple Choice)
4.8/5  (32)
(32)
Graph the ellipse. Give the coordinates of the center, as well as the values of and .
-
(Multiple Choice)
5.0/5  (35)
(35)
Most video games need to determine whether two objects touch, such as a character and a wall or a missile and an asteroid; this is known as collision detection. One method for doing this is to find a circle that bounds each object. If the distance between the centers of the two objects is less than or equal to the sum of the two radii of the circles that the objects are bounded by, the two objects are touching. Determine whether Object 1 with radius 9 pixels and center at touches Object 2 with radius 10 pixels and œenter at .
(True/False)
4.9/5  (36)
(36)
Find the center and radius of the circle by completing the square.
-
(Multiple Choice)
4.9/5  (31)
(31)
Showing 1 - 20 of 122
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)