Exam 9: Logarithmic and Exponential Functions
Exam 1: Review of Real Numbers152 Questions
Exam 2: Linear and Absolute Value Equations and Inequalities334 Questions
Exam 3: Graphing Linear Equations353 Questions
Exam 4: Systems of Equations204 Questions
Exam 5: Exponents, Polynomials, and Factoring Polynomials453 Questions
Exam 6: Rational Expressions and Equations249 Questions
Exam 7: Radical Expressions and Equations361 Questions
Exam 8: Quadratic Equations270 Questions
Exam 9: Logarithmic and Exponential Functions404 Questions
Exam 10: Conic Sections122 Questions
Exam 11: Sequences, Series, and the Binomial Theorem154 Questions
Select questions type
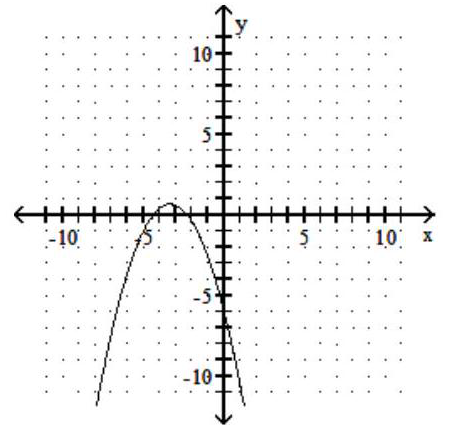
Determine whether the graph is the graph of a function.
-
Free
(True/False)
4.7/5  (32)
(32)
Correct Answer:
True
Given and , find the indicated composition and state its domain.
-
Find .
Free
(Multiple Choice)
4.8/5  (42)
(42)
Correct Answer:
D
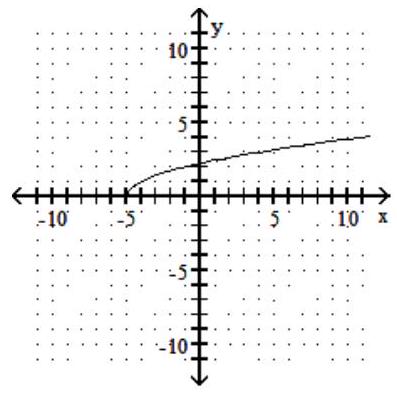
For the given graph of a one-to-one function f(x), graph its inverse functionf-1(x) using a dashed line
-
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
A
Solve the problem.
-A certain country's population , in millions, tyears after 2010 can be approximated by .
Find the doubling time. Round your answer to the nearest tenth.
(Multiple Choice)
4.8/5  (32)
(32)
The population growth of an animal species is described by where is the number of months since the species was introduced. Find the population of this species in an area 4 month(s) after the species is introduced.
(Multiple Choice)
4.7/5  (36)
(36)
Graph. State the domain, range, and vertical asymptote of the function
-
(Multiple Choice)
4.9/5  (39)
(39)
For the given functions and , find or as indicated.
-
Find .
(Multiple Choice)
4.8/5  (40)
(40)
For the given graph of a one-to-one function f(x), graph its inverse functionf-1(x) using a dashed line
-
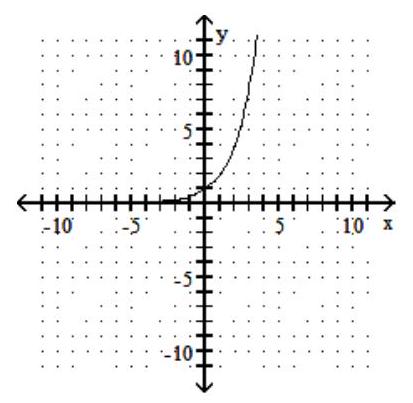
(Multiple Choice)
4.9/5  (28)
(28)
Given and , find the indicated composition and evaluate.
-
Find .
(Multiple Choice)
4.8/5  (27)
(27)
Find all intercepts for the given function. Round to the nearest tenth if necessary.
-
(Multiple Choice)
4.8/5  (35)
(35)
Solve.
-One method to determine the time since an animal died is to estimate the percentage of carbon- 14 remaining in its bones. The pencent in decimal form of carbon- 14 remaining years is given by . Approximate (to the nearest whole year) the age of a fossil if there is of carbon- 14 remaining.
(Multiple Choice)
4.8/5  (29)
(29)
Determine whether function is one-to-one.
-The function that pairs the temperature in degrees Fahrenheit of a cup of coffee with its temperature in degrees Celsius.
(True/False)
4.8/5  (38)
(38)
Solve the problem.
-Yearly sales of an electronic device S(t), in millions of dollars, tyears after 2009 can be estimated by
Determine the year in which sales reached million.
(Multiple Choice)
4.8/5  (36)
(36)
Compute the compound interest.
-John Lee's savings account has a balance of . After 5 years, what will the amount of interest be at compounded annually? Round to the nearest dollar.
(Multiple Choice)
4.9/5  (40)
(40)
Showing 1 - 20 of 404
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)