Exam 5: Exponents, Polynomials, and Polynomial Functions
Exam 1: Review of the Real Number System431 Questions
Exam 2: Linear Equations, Inequalities, and Applications338 Questions
Exam 3: Linear Equations, Graphs, and Functions347 Questions
Exam 4: Systems of Linear Equations166 Questions
Exam 5: Exponents, Polynomials, and Polynomial Functions327 Questions
Exam 6: Factoring180 Questions
Exam 7: Rational Expressions and Functions233 Questions
Exam 8: Roots, Radicals, and Root Functions358 Questions
Exam 9: Quadratic Equations, Inequalities, and Functions339 Questions
Exam 10: Inverse, Exponential, and Logarithmic Functions292 Questions
Exam 11: Nonlinear Functions, Conic Sections, and Nonlinear Systems233 Questions
Exam 12: Further Topics in Algebra190 Questions
Exam 13: Appendices29 Questions
Select questions type
For the given pair of functions, find the requested function.
-
(Multiple Choice)
4.8/5  (42)
(42)
Write the expression with only positive exponents. Assume all variables represent nonzero numbers. Simplify if necessary.
-
(Multiple Choice)
4.8/5  (44)
(44)
Apply the quotient rule for exponents, if applicable, and write the result using only positive exponents. Assume all variables represent nonzero numbers.
-
(Multiple Choice)
4.7/5  (45)
(45)
Simplify the expression. Write your answer with only positive exponents. Assume that all variables represent nonzero real numbers.
-
(Multiple Choice)
4.9/5  (35)
(35)
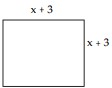
Express the area of the figure as a polynomial in descending powers of the variable .
-
(Multiple Choice)
4.8/5  (31)
(31)
Choose the one alternative that best completes the statement or answers the question.
Divide
-
(Multiple Choice)
4.8/5  (33)
(33)
The polynomial gives the approximate total earnings of a company, in millions of dollars, where corresponds to corresponds to 1997 , and so on. This model is valid for the years from 1996 to 2000. Determine the earnings for 1999. Round your answer to the nearest hundredth million.
(Multiple Choice)
4.8/5  (32)
(32)
Tell whether the statement is .
-A monomial has no coefficient.
(Multiple Choice)
4.8/5  (42)
(42)
The polynomial gives the predicted sales volume of a company, in millions of items, where is the number of years from now. Determine the predicted sales 9 years from now. Round your answer to the nearest hundredth million.
(Multiple Choice)
4.7/5  (37)
(37)
For the pair of functions, find the quotient and give any -values that are not in the domain of the quotient function.
-
(Multiple Choice)
4.8/5  (41)
(41)
Showing 61 - 80 of 327
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)