Exam 4: Linear Programming Models

Exhibit 4-3 A meat market manager for a large grocery store is preparing a processing plan to stock the shelves with sausage, ground meat, and jerky, which he can prepare from beef, pork and venison. Sausage and ground meat can be made of any mix of the beef, pork and venison, as long at the fat contents are below 15% for sausage and 10% for ground meat. Sausage sells for $5/pound and ground meat sells for $3/pound. Jerky, which sells or $10/pound, is made in a drying process from beef or venison. In the drying process, there is a 50% loss in weight for jerky made from beef (e.g., one pound of beef yields 0.5 pounds of beef jerky) and a 20% loss in weight for jerky made from venison. The market can sell at most 500 pounds of sausage, 1000 pounds of ground meat, and 100 pounds of jerky before their expiration dates. There are currently 1,000 pounds of beef (10% fat content), 500 pounds of pork (8% fat content), and 200 pounds of venison (2% fat content) available for processing. -[Part 1] Refer to Exhibit 4-3. Suppose that later in the year, venison will be out of season, but the market will be able to obtain an additional 300 pounds of pork for the same costs. Develop a processing plan in that case. How does the solution change?

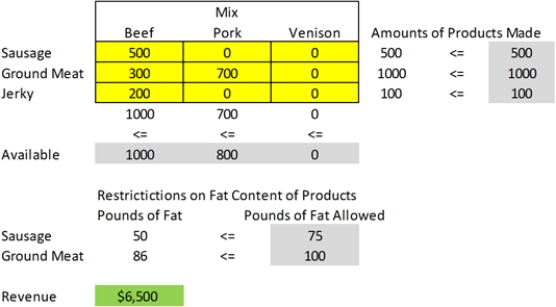
Exhibit 4-2A construction company is preparing for a nine-month project, and will need to develop a staffing plan. The company can assign up to 30 of its own full-time employees to the project, and will hire short-term contract employees to make up any shortage in meeting the personnel requirements. Company employees earn $6,000 per month, while short-term contract employees make $8,600/month. Contract employees can be assigned to the project beginning in any month, and their contract period is two months. The number of workers required for the project by month is shown below: Month of Project 1 2 3 4 5 6 7 8 9 Required 15 23 59 65 71 77 64 43 21 -Refer to Exhibit 4-2. Determine the optimal staffing plan for the project.

Workforce scheduling problems in which the worker schedules continue week to week are:

Exhibit 4-3 A meat market manager for a large grocery store is preparing a processing plan to stock the shelves with sausage, ground meat, and jerky, which he can prepare from beef, pork and venison. Sausage and ground meat can be made of any mix of the beef, pork and venison, as long at the fat contents are below 15% for sausage and 10% for ground meat. Sausage sells for $5/pound and ground meat sells for $3/pound. Jerky, which sells or $10/pound, is made in a drying process from beef or venison. In the drying process, there is a 50% loss in weight for jerky made from beef (e.g., one pound of beef yields 0.5 pounds of beef jerky) and a 20% loss in weight for jerky made from venison. The market can sell at most 500 pounds of sausage, 1000 pounds of ground meat, and 100 pounds of jerky before their expiration dates. There are currently 1,000 pounds of beef (10% fat content), 500 pounds of pork (8% fat content), and 200 pounds of venison (2% fat content) available for processing. -Refer to Exhibit 4-3. Determine the optimal processing plan for the meat market.

If integer constraints are used in a model, Solver uses an algorithm called branch and round to obtain the solution.

If we round the optimal values in the changing cells of a linear programming model, this is a good approximation of the integer programming solution.

In aggregate planning models, which of the following statements are correct?

Problems in which we must determine how to schedule employees to provide adequate service under the same situation each planning period are referred to as:

Integer programming (IP) models are optimization models in which all of the variables must be integers.

Exhibit 4-2A construction company is preparing for a nine-month project, and will need to develop a staffing plan. The company can assign up to 30 of its own full-time employees to the project, and will hire short-term contract employees to make up any shortage in meeting the personnel requirements. Company employees earn $6,000 per month, while short-term contract employees make $8,600/month. Contract employees can be assigned to the project beginning in any month, and their contract period is two months. The number of workers required for the project by month is shown below: Month of Project 1 2 3 4 5 6 7 8 9 Required 15 23 59 65 71 77 64 43 21 -Refer to Exhibit 4-2. Suppose the bonus for completing the project three months early is $250,000. What would be the net bonus to the company, after adjusting for any difference in personnel costs under the accelerated schedule?

The constraints in a blending problem can be specified in a valid way and still lead to which of the following problems?

In aggregate planning models, we can model backlogging of demand by allowing a month's inventory to be negative.

The results of a sensitivity analysis with a dual objective model can be shown graphically using a:

Exhibit 4-4 A company blends nitrogen and phosphorous to produce two types of fertilizers. Fertilizer 1 must be at least 50% nitrogen and sells for $55 per pound. Fertilizer 2 must be at least 55% phosphorous and sells for $45 per pound. The company can purchase up to 9000 pounds of nitrogen at $20 per pound and up to 12,000 pounds of phosphorous at $12 per pound. -Refer to Exhibit 4-4. Assuming that all fertilizer produced can be sold, determine the optimal blending plan for the company. What is the maximum profit?

To specify that X1 must be at most 75% of the blend of X1, X2, and X3, we must have a constraint of the form

One way to solve a dual-objective problem is to use one objective as the target cell and constrain the other.

Aggregate planning models usually relate a beginning value in one period to an ending value from the previous period.

Which of the following statements is a type of constraint that is often required in blending problems?

Exhibit 4-3 A meat market manager for a large grocery store is preparing a processing plan to stock the shelves with sausage, ground meat, and jerky, which he can prepare from beef, pork and venison. Sausage and ground meat can be made of any mix of the beef, pork and venison, as long at the fat contents are below 15% for sausage and 10% for ground meat. Sausage sells for $5/pound and ground meat sells for $3/pound. Jerky, which sells or $10/pound, is made in a drying process from beef or venison. In the drying process, there is a 50% loss in weight for jerky made from beef (e.g., one pound of beef yields 0.5 pounds of beef jerky) and a 20% loss in weight for jerky made from venison. The market can sell at most 500 pounds of sausage, 1000 pounds of ground meat, and 100 pounds of jerky before their expiration dates. There are currently 1,000 pounds of beef (10% fat content), 500 pounds of pork (8% fat content), and 200 pounds of venison (2% fat content) available for processing. -[Part 2] Refer to Exhibit 4-3. What happens to the revenue when the optimal plan changes to the one given in Part 1?

Exhibit 4-1A hospital emergency room requires different numbers of nurses on different days of the week. The number of full-time employees required to be working (i.e. not on call) each day is given in the table below. Hospital rules require that nurses work four consecutive days, are on call for one day, and then receive two days off. The hospital wants to meet its daily requirements, while minimizing the number of nurses that must be on staff. Mon Tue Wed Thu Fri Sat Sun 18 15 12 13 20 28 22 -Refer to Exhibit 4-1. Suppose the hospital is experiencing a budget crunch and needs to use the nurses' on call day to temporarily staff the emergency room. Use Solver to formulate and solve the hospital's problem.