Exam 5: Network Models
Exam 1: Introduction to Modeling30 Questions
Exam 2: Introduction to Spreadsheet Modeling30 Questions
Exam 3: Introduction to Optimization Modeling30 Questions
Exam 4: Linear Programming Models31 Questions
Exam 5: Network Models30 Questions
Exam 6: Optimization Models With Integer Variables30 Questions
Exam 7: Nonlinear Optimization Models30 Questions
Exam 8: Evolutionary Solver: An Alternative Optimization Procedure30 Questions
Exam 9: Decision Making Under Uncertainty30 Questions
Exam 10: Introduction to Simulation Modeling30 Questions
Exam 11: Simulation Models30 Questions
Exam 12: Inventory and Supply Chain Models30 Questions
Exam 13: Queuing Models30 Questions
Exam 14: Regression and Forecasting Models30 Questions
Select questions type
It is useful to model network problems by listing all of the arcs and their corresponding flows in one long, comprehensive list.
Free
(True/False)
4.7/5  (29)
(29)
Correct Answer:
True
Exhibit 5-1Sinclair Plastics operates two chemical plants which produce polyethylene; the Ohio Valley plant which can produce up to 10,000 tons per month and the Lakeview plant which can produce up to 7,000 tons per month. Sinclair sells its polyethylene to three different auto manufacturing plants, Grand Rapids (demand = 3000 tons per month), Blue Ridge (demand = 5000 tons per month), and Sunset (demand = 4000 tons per month). The costs of shipping between the respective plants is shown in the table below:
 -Refer to Exhibit 5-1. Implement the LP model in Solver and obtain the optimal shipping plan. What is the optimized cost?
-Refer to Exhibit 5-1. Implement the LP model in Solver and obtain the optimal shipping plan. What is the optimized cost?
Free
(Essay)
4.8/5  (27)
(27)
Correct Answer:
The optimized model below shows the shipping plan, which results in a total cost of $650,000.
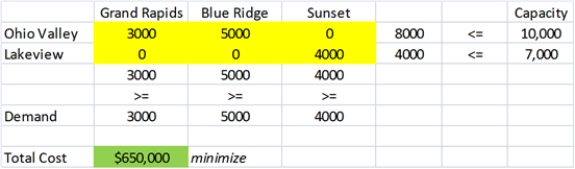
Exhibit 5-3Steve the auto parts salesman is trying to navigate his way between the rural west Texas towns of Jonestown and Upland. The possible routes for this trip are shown below, along with the mileage along each route.
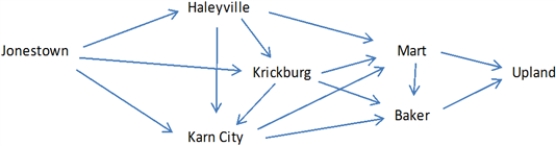 Origin Destination Distance (miles) Jonestown to Haleyville 25 Jonestown to Krickburg 55 Jonestown to Karn City 35 Haleyville to Mart 50 Haleyville to Krickburg 25 Haleyville to Karn City 30 Karn City to Mart 50 Karn City to Baker 65 Krickburg to Karn City 20 Krickburg to Baker 30 Krickburg to Mart 45 Mart to Baker 20 Mart to Upland 40 Baker to Upland 30
-Refer to Exhibit 5-3. Suppose the roads leading into and out of Krickburg are unpaved, so Steve would only be able to travel half of his usual 60 mile/hour speed on those routes. Modify the model to account for this condition. Would the shortest path change from the base case solution?
Origin Destination Distance (miles) Jonestown to Haleyville 25 Jonestown to Krickburg 55 Jonestown to Karn City 35 Haleyville to Mart 50 Haleyville to Krickburg 25 Haleyville to Karn City 30 Karn City to Mart 50 Karn City to Baker 65 Krickburg to Karn City 20 Krickburg to Baker 30 Krickburg to Mart 45 Mart to Baker 20 Mart to Upland 40 Baker to Upland 30
-Refer to Exhibit 5-3. Suppose the roads leading into and out of Krickburg are unpaved, so Steve would only be able to travel half of his usual 60 mile/hour speed on those routes. Modify the model to account for this condition. Would the shortest path change from the base case solution?
Free
(Essay)
4.9/5  (37)
(37)
Correct Answer:
The revised shortest path (in minutes) is shown below. Steve will now travel 115 miles (i.e., 115 minutes @ 60 miles per hour) and Krickburg is no longer on his route.
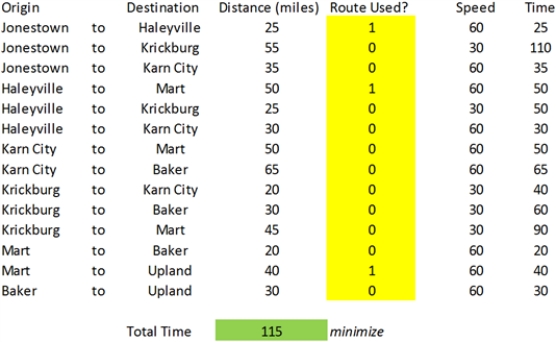
Exhibit 5-3Steve the auto parts salesman is trying to navigate his way between the rural west Texas towns of Jonestown and Upland. The possible routes for this trip are shown below, along with the mileage along each route.
 Origin Destination Distance (miles) Jonestown to Haleyville 25 Jonestown to Krickburg 55 Jonestown to Karn City 35 Haleyville to Mart 50 Haleyville to Krickburg 25 Haleyville to Karn City 30 Karn City to Mart 50 Karn City to Baker 65 Krickburg to Karn City 20 Krickburg to Baker 30 Krickburg to Mart 45 Mart to Baker 20 Mart to Upland 40 Baker to Upland 30
-Refer to Exhibit 5-3. What general type of LP model can be applied to this problem? What modifications to the general type are required for this problem?
Origin Destination Distance (miles) Jonestown to Haleyville 25 Jonestown to Krickburg 55 Jonestown to Karn City 35 Haleyville to Mart 50 Haleyville to Krickburg 25 Haleyville to Karn City 30 Karn City to Mart 50 Karn City to Baker 65 Krickburg to Karn City 20 Krickburg to Baker 30 Krickburg to Mart 45 Mart to Baker 20 Mart to Upland 40 Baker to Upland 30
-Refer to Exhibit 5-3. What general type of LP model can be applied to this problem? What modifications to the general type are required for this problem?
(Essay)
4.9/5  (28)
(28)
Exhibit 5-1Sinclair Plastics operates two chemical plants which produce polyethylene; the Ohio Valley plant which can produce up to 10,000 tons per month and the Lakeview plant which can produce up to 7,000 tons per month. Sinclair sells its polyethylene to three different auto manufacturing plants, Grand Rapids (demand = 3000 tons per month), Blue Ridge (demand = 5000 tons per month), and Sunset (demand = 4000 tons per month). The costs of shipping between the respective plants is shown in the table below:
 -Refer to Exhibit 5-1. Formulate (write out algebraically) an LP transportation model to help Sinclair minimize its shipping costs.
-Refer to Exhibit 5-1. Formulate (write out algebraically) an LP transportation model to help Sinclair minimize its shipping costs.
(Essay)
4.7/5  (36)
(36)
Exhibit 5-3Steve the auto parts salesman is trying to navigate his way between the rural west Texas towns of Jonestown and Upland. The possible routes for this trip are shown below, along with the mileage along each route.
 Origin Destination Distance (miles) Jonestown to Haleyville 25 Jonestown to Krickburg 55 Jonestown to Karn City 35 Haleyville to Mart 50 Haleyville to Krickburg 25 Haleyville to Karn City 30 Karn City to Mart 50 Karn City to Baker 65 Krickburg to Karn City 20 Krickburg to Baker 30 Krickburg to Mart 45 Mart to Baker 20 Mart to Upland 40 Baker to Upland 30
-Refer to Exhibit 5-3. Implement the appropriate model in Solver and determine the shortest path for Steve. How many total miles will he travel on his trip?
Origin Destination Distance (miles) Jonestown to Haleyville 25 Jonestown to Krickburg 55 Jonestown to Karn City 35 Haleyville to Mart 50 Haleyville to Krickburg 25 Haleyville to Karn City 30 Karn City to Mart 50 Karn City to Baker 65 Krickburg to Karn City 20 Krickburg to Baker 30 Krickburg to Mart 45 Mart to Baker 20 Mart to Upland 40 Baker to Upland 30
-Refer to Exhibit 5-3. Implement the appropriate model in Solver and determine the shortest path for Steve. How many total miles will he travel on his trip?
(Essay)
4.9/5  (40)
(40)
Exhibit 5-2A small engineering firm employs one civil engineer, two engineering technicians, and one summer intern. The types of projects the firm does includes surveys (typically 7 per month), designs (5 per month), and construction project plans (four per month). The times, in hours, required for each employee to complete teach type of project are shown below. Based on their capabilities and time spent on travel and administrative tasks, the engineer, tech 1, tech 2, and intern can handle 5, 4, 4, and 3 projects per month, respectively.
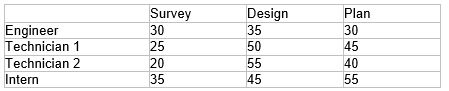 -Refer to Exhibit 5-2. Based on their salaries, the engineer, tech 1, tech 2, and intern earn $90, $65, $65, and $45 per hourly, respectively. Change the firm's objective function to minimize staff costs and find the optimal assignment plan. Does it change from the base case?
-Refer to Exhibit 5-2. Based on their salaries, the engineer, tech 1, tech 2, and intern earn $90, $65, $65, and $45 per hourly, respectively. Change the firm's objective function to minimize staff costs and find the optimal assignment plan. Does it change from the base case?
(Essay)
4.9/5  (34)
(34)
Exhibit 5-1Sinclair Plastics operates two chemical plants which produce polyethylene; the Ohio Valley plant which can produce up to 10,000 tons per month and the Lakeview plant which can produce up to 7,000 tons per month. Sinclair sells its polyethylene to three different auto manufacturing plants, Grand Rapids (demand = 3000 tons per month), Blue Ridge (demand = 5000 tons per month), and Sunset (demand = 4000 tons per month). The costs of shipping between the respective plants is shown in the table below:
 -Refer to Exhibit 5-1. Suppose the shipping capacity between any two plants was limited to 2500 tons per month. Design and implement a network flow version of this model in Solver and obtain the optimal shipping plan. How much more would the shipping plan cost Sinclair in that case?
-Refer to Exhibit 5-1. Suppose the shipping capacity between any two plants was limited to 2500 tons per month. Design and implement a network flow version of this model in Solver and obtain the optimal shipping plan. How much more would the shipping plan cost Sinclair in that case?
(Essay)
4.8/5  (35)
(35)
In transportation problems, shipments between supply points or between demand points are possible.
(True/False)
4.8/5  (40)
(40)
In a minimum cost network flow model, the flow balance constraint for each supply node has the form
(Multiple Choice)
4.8/5  (39)
(39)
In network models of transportation problems, arcs represent the routes for getting a product from one node to another.
(True/False)
4.9/5  (32)
(32)
For all routes with positive flows in an optimized transportation problem, the reduced cost will be:
(Multiple Choice)
4.8/5  (37)
(37)
Problems which deal with the direct distribution of products from supply locations to demand locations are called:
(Multiple Choice)
4.7/5  (40)
(40)
Which of the following is not an example of a condition that a more complex logistics model might include?
(Multiple Choice)
4.9/5  (30)
(30)
A particularly useful Excel function in the formulation of transportation problems is the:
(Multiple Choice)
4.8/5  (43)
(43)
The network model representation of the transportation problem has the following advantage relative to the special case of a simple transportation model:
(Multiple Choice)
4.7/5  (35)
(35)
The flow balance constraint for each transshipment node in a network flow model has the form Flow in = Flow out.
(True/False)
4.8/5  (39)
(39)
In an assignment model of machines to jobs, the machines are analogous to which of the following in a transportation problem?
(Multiple Choice)
4.9/5  (28)
(28)
Transshipment points are locations where goods neither originate nor end up, but goods are allowed to enter such points to be shipped out to their eventual destinations.
(True/False)
4.9/5  (29)
(29)
Showing 1 - 20 of 30
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)