Exam 17: A: Technology
Exam 1: Budget Constraint58 Questions
Exam 1: A: Budget Constraint30 Questions
Exam 2: Preferences49 Questions
Exam 2: A: Preferences30 Questions
Exam 3: Utility57 Questions
Exam 3: A: Utility29 Questions
Exam 4: Choice63 Questions
Exam 4: A: Choice31 Questions
Exam 5: Demand79 Questions
Exam 5: A: Demand22 Questions
Exam 6: Revealed Preference58 Questions
Exam 6: A: Revealed Preference26 Questions
Exam 7: Slutsky Equation51 Questions
Exam 7: A: Slutsky Equation30 Questions
Exam 8: Buying and Selling75 Questions
Exam 8: A: Buying and Selling30 Questions
Exam 9: Intertemporal Choice61 Questions
Exam 9: A: Intertemporal Choice30 Questions
Exam 10: Asset Markets46 Questions
Exam 10: A: Asset Markets30 Questions
Exam 11: Uncertainty39 Questions
Exam 11: A: Uncertainty25 Questions
Exam 12: Risky Assets16 Questions
Exam 12: A: Risky Assets10 Questions
Exam 13: Consumers Surplus42 Questions
Exam 13: A: Consumers Surplus30 Questions
Exam 14: Market Demand101 Questions
Exam 14: A: Market Demand25 Questions
Exam 15: Equilibrium48 Questions
Exam 15: A: Equilibrium20 Questions
Exam 16: Auctions36 Questions
Exam 16: A: Auctions25 Questions
Exam 17: Technology52 Questions
Exam 17: A: Technology30 Questions
Exam 18: Profit Maximization52 Questions
Exam 18: A: Profit Maximization21 Questions
Exam 19: Cost Minimization77 Questions
Exam 19: A: Cost Minimization26 Questions
Exam 20: Cost Curves51 Questions
Exam 20: A: Cost Curves20 Questions
Exam 21: Firm Supply41 Questions
Exam 21: A: Firm Supply15 Questions
Exam 22: Industry Supply49 Questions
Exam 22: A: Industry Supply33 Questions
Exam 23: Monopoly76 Questions
Exam 23: A: Monopoly30 Questions
Exam 24: Monopoly Behavior34 Questions
Exam 24: A: Monopoly Behavior20 Questions
Exam 25: Factor Markets24 Questions
Exam 25: A: Factor Markets20 Questions
Exam 26: Oligopoly56 Questions
Exam 26: A: Oligopoly30 Questions
Exam 27: Game Theory34 Questions
Exam 27: A: Game Theory25 Questions
Exam 28: Game Applications28 Questions
Exam 28: A: Game Applications25 Questions
Exam 29: Behavioral Economics34 Questions
Exam 30: Exchange68 Questions
Exam 30: A: Exchange30 Questions
Exam 31: Production35 Questions
Exam 31: A: Production25 Questions
Exam 32: Welfare27 Questions
Exam 32: A: Welfare25 Questions
Exam 33: Externalities42 Questions
Exam 33: A: Externalities25 Questions
Exam 34: Information Technology24 Questions
Exam 34: A: Information Technology15 Questions
Exam 35: Public Goods26 Questions
Exam 35: A: Public Goods20 Questions
Exam 36: Asymmetric Information31 Questions
Exam 36: A: Asymmetric Information20 Questions
Select questions type
A firm uses 3 factors of production. Its production function is f(x, y, z) = min{ 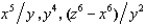 }. If the amount of each input is multiplied by 3, its output will be multiplied by
}. If the amount of each input is multiplied by 3, its output will be multiplied by
Free
(Multiple Choice)
4.8/5  (40)
(40)
Correct Answer:
A
A firm has the production function f(x, y) = x1.10y1. This firm has
Free
(Multiple Choice)
4.7/5  (40)
(40)
Correct Answer:
E
This problem will be easier if you have done Problem 1. A firm has the production function $f(x1, x2) = x0.401x0.202. The isoquant on which output is 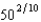 has the equation
has the equation
Free
(Multiple Choice)
4.8/5  (45)
(45)
Correct Answer:
D
In Problem 8, if a = 2.40, b = 0.50, and c = 1, the marginal products of x1, x2, and x3 (in this order) are
(Multiple Choice)
4.8/5  (40)
(40)
In Problem 3, if the exponents in the production function were 0.30 for x1 and 0.20 for x2, this production function would exhibit (constant, increasing, decreasing) returns to scale and (would, would not) have diminishing technical rate of substitution.
(Multiple Choice)
4.8/5  (32)
(32)
A firm has the production function f(x, y) = x1.40y1.90. This firm has
(Multiple Choice)
4.9/5  (32)
(32)
In Problem 3, if the exponents in the production function were 0.40 for x1 and 0.40 for x2, this production function would exhibit (constant, increasing, decreasing) returns to scale and (would, would not) have diminishing technical rate of substitution.
(Multiple Choice)
4.9/5  (43)
(43)
A firm has a production function f(x, y) = 1.80(x0.80 + y0.80)1 whenever x > 0 and y > 0. When the amounts of both inputs are positive, this firm has
(Multiple Choice)
4.7/5  (44)
(44)
In Problem 3, if the exponents in the production function were 0.30 for x1 and 0.30 for x2, this production function would exhibit (constant, increasing, decreasing) returns to scale and (would, would not) have diminishing technical rate of substitution.
(Multiple Choice)
4.9/5  (39)
(39)
A firm has a production function f(x, y) = 0.70(x0.20 + y0.20)4 whenever x > 0 and y > 0. When the amounts of both inputs are positive, this firm has
(Multiple Choice)
5.0/5  (37)
(37)
A firm has the production function f(x, y) = x1.20y2. This firm has
(Multiple Choice)
4.8/5  (28)
(28)
A firm has a production function f(x, y) = 0.70(x0.80 + y0.80)2 whenever x > 0 and y > 0. When the amounts of both inputs are positive, this firm has
(Multiple Choice)
4.8/5  (40)
(40)
In Problem 3, if the exponents in the production function were 0.60 for x1 and 0.40 for x2, this production function would exhibit (constant, increasing, decreasing) returns to scale and (would, would not) have diminishing technical rate of substitution.
(Multiple Choice)
4.8/5  (37)
(37)
In Problem 8, if a = 2.10, b = 0.40, and c = 1, the marginal products of x1, x2, and x3 (in this order) are
(Multiple Choice)
4.7/5  (39)
(39)
A firm has the production function f(x, y) = x1.40y1.40. This firm has
(Multiple Choice)
4.7/5  (43)
(43)
A firm uses 3 factors of production. Its production function is f(x, y, z) = min{ 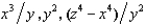 }. If the amount of each input is multiplied by 6, its output will be multiplied by
}. If the amount of each input is multiplied by 6, its output will be multiplied by
(Multiple Choice)
4.9/5  (30)
(30)
In Problem 3, if the exponents in the production function were 0.80 for x1 and 0.20 for x2, this production function would exhibit (constant, increasing, decreasing) returns to scale and (would, would not) have diminishing technical rate of substitution.
(Multiple Choice)
4.8/5  (34)
(34)
In Problem 8, if a = 2.10, b = 1.10, and c = 1.20, the marginal products of x1, x2, and x3 (in this order) are
(Multiple Choice)
4.8/5  (30)
(30)
This problem will be easier if you have done Problem 1. A firm has the production function $f(x1, x2) = x0.501x0.102. The isoquant on which output is 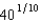 has the equation
has the equation
(Multiple Choice)
4.7/5  (38)
(38)
A firm uses 3 factors of production. Its production function is f(x, y, z) = min{ 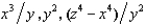 }. If the amount of each input is multiplied by 6, its output will be multiplied by
}. If the amount of each input is multiplied by 6, its output will be multiplied by
(Multiple Choice)
5.0/5  (36)
(36)
Showing 1 - 20 of 30
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)