Exam 11: Uncertainty
Exam 1: Budget Constraint58 Questions
Exam 1: A: Budget Constraint30 Questions
Exam 2: Preferences49 Questions
Exam 2: A: Preferences30 Questions
Exam 3: Utility57 Questions
Exam 3: A: Utility29 Questions
Exam 4: Choice63 Questions
Exam 4: A: Choice31 Questions
Exam 5: Demand79 Questions
Exam 5: A: Demand22 Questions
Exam 6: Revealed Preference58 Questions
Exam 6: A: Revealed Preference26 Questions
Exam 7: Slutsky Equation51 Questions
Exam 7: A: Slutsky Equation30 Questions
Exam 8: Buying and Selling75 Questions
Exam 8: A: Buying and Selling30 Questions
Exam 9: Intertemporal Choice61 Questions
Exam 9: A: Intertemporal Choice30 Questions
Exam 10: Asset Markets46 Questions
Exam 10: A: Asset Markets30 Questions
Exam 11: Uncertainty39 Questions
Exam 11: A: Uncertainty25 Questions
Exam 12: Risky Assets16 Questions
Exam 12: A: Risky Assets10 Questions
Exam 13: Consumers Surplus42 Questions
Exam 13: A: Consumers Surplus30 Questions
Exam 14: Market Demand101 Questions
Exam 14: A: Market Demand25 Questions
Exam 15: Equilibrium48 Questions
Exam 15: A: Equilibrium20 Questions
Exam 16: Auctions36 Questions
Exam 16: A: Auctions25 Questions
Exam 17: Technology52 Questions
Exam 17: A: Technology30 Questions
Exam 18: Profit Maximization52 Questions
Exam 18: A: Profit Maximization21 Questions
Exam 19: Cost Minimization77 Questions
Exam 19: A: Cost Minimization26 Questions
Exam 20: Cost Curves51 Questions
Exam 20: A: Cost Curves20 Questions
Exam 21: Firm Supply41 Questions
Exam 21: A: Firm Supply15 Questions
Exam 22: Industry Supply49 Questions
Exam 22: A: Industry Supply33 Questions
Exam 23: Monopoly76 Questions
Exam 23: A: Monopoly30 Questions
Exam 24: Monopoly Behavior34 Questions
Exam 24: A: Monopoly Behavior20 Questions
Exam 25: Factor Markets24 Questions
Exam 25: A: Factor Markets20 Questions
Exam 26: Oligopoly56 Questions
Exam 26: A: Oligopoly30 Questions
Exam 27: Game Theory34 Questions
Exam 27: A: Game Theory25 Questions
Exam 28: Game Applications28 Questions
Exam 28: A: Game Applications25 Questions
Exam 29: Behavioral Economics34 Questions
Exam 30: Exchange68 Questions
Exam 30: A: Exchange30 Questions
Exam 31: Production35 Questions
Exam 31: A: Production25 Questions
Exam 32: Welfare27 Questions
Exam 32: A: Welfare25 Questions
Exam 33: Externalities42 Questions
Exam 33: A: Externalities25 Questions
Exam 34: Information Technology24 Questions
Exam 34: A: Information Technology15 Questions
Exam 35: Public Goods26 Questions
Exam 35: A: Public Goods20 Questions
Exam 36: Asymmetric Information31 Questions
Exam 36: A: Asymmetric Information20 Questions
Select questions type
Sally Kink is an expected utility maximizer with utility function pu(c1) + (1 - p)u(c2), where for any x < $2,000, u(x) = 2x, and for x greater than or equal to $2,000, u(x) = 2,000 + x.
Free
(Multiple Choice)
5.0/5  (37)
(37)
Correct Answer:
A
An expected utility maximizer's preferences between two bundles contingent on event 1 happening must be independent of what he will get if event 2 happens.
Free
(True/False)
4.7/5  (35)
(35)
Correct Answer:
True
The certainty equivalent of a gamble is defined to be the amount of money which, if you were promised it with certainty, would be indifferent to the gamble.
a. If an expected utility maximizer has a von Neuman-Morgenstern utility function U(W) = W 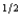 (where W is wealth) and if the probability of events 1 and 2 are both
(where W is wealth) and if the probability of events 1 and 2 are both 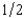 , write a formula for the certainty equivalent of a gamble that gives you x if event 1 happens and y if event 2 happens.
b. Generalize your formula in part (a) to the case where the probability of event 1 is p and the probability of event 2 is 1 - p.
c. Generalize the formula in part (a) to the case where U(W) = Wa for a > 0.
, write a formula for the certainty equivalent of a gamble that gives you x if event 1 happens and y if event 2 happens.
b. Generalize your formula in part (a) to the case where the probability of event 1 is p and the probability of event 2 is 1 - p.
c. Generalize the formula in part (a) to the case where U(W) = Wa for a > 0.
Free
(Essay)
4.8/5  (33)
(33)
Correct Answer:
a. The certainty equivalent is 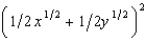 b.
b. 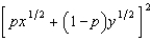 c.
c. 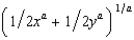
Socrates owns just one ship. The ship is worth $200 million dollars. If the ship sinks, Socrates loses $200 million. The probability that it will sink is .02. Socrates' total wealth including the value of the ship is $225 million. He is an expected utility maximizer with von Neuman-Morgenstern utility U(W) equal to the square root of W. What is the maximum amount that Socrates would be willing to pay in order to be fully insured against the risk of losing his ship?
(Multiple Choice)
4.9/5  (40)
(40)
Ronald has $18,000. But he is forced to bet it on the flip of a fair coin. If he wins he has $36,000. If he loses he has nothing. Ronald's expected utility function is .5x.5 + .5y.5, where x is his wealth if heads comes up and y is his wealth if tails comes up. Since he must make this bet, he is exactly as well off as if he had a perfectly safe income of
(Multiple Choice)
4.8/5  (37)
(37)
Oskar's preferences over gambles in which the probability of events 1 and 2 are both 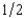 can be represented by the von Neuman-Morgenstern utility function .5y.51 + .5y.52, where y1 is his consumption if event 1 happens and y2 is his consumption if event 2 happens. A gamble that allows him a consumption of $9 if event 1 happens and $25 if event 2 happens is exactly as good for Oskar as being sure to have an income of
can be represented by the von Neuman-Morgenstern utility function .5y.51 + .5y.52, where y1 is his consumption if event 1 happens and y2 is his consumption if event 2 happens. A gamble that allows him a consumption of $9 if event 1 happens and $25 if event 2 happens is exactly as good for Oskar as being sure to have an income of
(Multiple Choice)
4.8/5  (43)
(43)
Of any two gambles, no matter what their expected returns, a risk averter will choose the one with the smaller variance.
(True/False)
4.8/5  (39)
(39)
Mabel and Emil were contemplating marriage. They got to talking. Mabel said that she always acted according to the expected utility hypothesis, where she tried to maximize the expected value of the log of her income. Emil said that he too was an expected utility maximizer, but he tried to maximize the expected value of the square of his income. Mabel said, "I fear we must part. Our attitudes toward risk are too different." Emil said, "Never fear, my dear, the square of income is a monotonic increasing function of the log of income, so we really have the same preferences." Who is right about whether their preferences toward risk are different?
(Multiple Choice)
4.8/5  (31)
(31)
Joe's wealth is $100 and he is an expected utility maximizer with a von Neumann-Morgenstern utility function 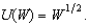 Joe is afraid of oversleeping his economics exam. He figures there is only a 1 in 10 chance that he will, but if he does, it will cost him $100 in fees to the university for taking an exam late. Joe's neighbor, Mary, never oversleeps. She offers to wake him one hour before the test, but he must pay her for this service. What is the most that Joe would be willing to pay for this wake-up service?
Joe is afraid of oversleeping his economics exam. He figures there is only a 1 in 10 chance that he will, but if he does, it will cost him $100 in fees to the university for taking an exam late. Joe's neighbor, Mary, never oversleeps. She offers to wake him one hour before the test, but he must pay her for this service. What is the most that Joe would be willing to pay for this wake-up service?
(Multiple Choice)
4.8/5  (41)
(41)
If the price of insurance goes up, people will become less risk averse.
(True/False)
4.9/5  (34)
(34)
Yoram's expected utility function is pc 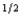 1 + (1 - p)c
1 + (1 - p)c 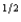 2, where p is the probability that he consumes c1 and 1 - p is the probability that he consumes c2. Wilbur is offered a choice between getting a sure payment of $Z or a lottery in which he receives $2,500 with probability .30 and $3,600 with probability .70. Wilbur will choose the sure payment if
2, where p is the probability that he consumes c1 and 1 - p is the probability that he consumes c2. Wilbur is offered a choice between getting a sure payment of $Z or a lottery in which he receives $2,500 with probability .30 and $3,600 with probability .70. Wilbur will choose the sure payment if
(Multiple Choice)
4.9/5  (26)
(26)
A consumer has a von Neumann-Morgenstern utility function of the form U(cA, cB, pA, pB) = pAv(cA) + pBv(cB), where pA and pB are the probabilities of events A and B and where cA and cB are consumptions contingent on events A and B respectively. This consumer must be a risk lover if v is an increasing function.
(True/False)
4.8/5  (28)
(28)
Buck Columbus is thinking of starting a pinball palace near a large Midwestern university. Buck is an expected utility maximizer with a von Neuman-Morgenstern utility function, U(W) = 1 - ( 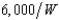 ), where W is his wealth. Buck's total wealth is $24,000. With probability .2 the palace will be a failure and he'll lose $18,000, so that his wealth will be just $6,000. With probability .8 it will succeed and his wealth will grow to $x. What is the smallest value of x that would be sufficient to make Buck want to invest in the pinball palace rather than have a wealth of $24,000 with certainty?
), where W is his wealth. Buck's total wealth is $24,000. With probability .2 the palace will be a failure and he'll lose $18,000, so that his wealth will be just $6,000. With probability .8 it will succeed and his wealth will grow to $x. What is the smallest value of x that would be sufficient to make Buck want to invest in the pinball palace rather than have a wealth of $24,000 with certainty?
(Multiple Choice)
4.9/5  (37)
(37)
Portia has waited a long time for her ship to come in, and she has concluded that it will arrive today with probability 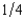 . If it does come, she will receive $16. If it doesn't come in today, it never will and she will have zero wealth. She has a von Neumann-Morgenstern utility function equal to the square root of her total income. What is the minimum price at which she would sell the rights to her ship?
. If it does come, she will receive $16. If it doesn't come in today, it never will and she will have zero wealth. She has a von Neumann-Morgenstern utility function equal to the square root of her total income. What is the minimum price at which she would sell the rights to her ship?
(Multiple Choice)
4.7/5  (43)
(43)
After graduating, Sallie Handshake's best job offer will either be with a Big-8 accounting firm for $160,000 a year or as a State Farm agent in Grand Rapids, Michigan, for $40,000 a year. She can increase the probability of the former outcome by studying more, but such studying has its costs. If S represents her amount of studying (where S = 0 is no study and S = 1 is all-out effort), her probability of getting the job with a Big-8 firm just equals S. Her utility depends on how hard she studies and her subsequent annual income Y. She tries to maximize the expected value of the von Neuman-Morgenstern utility function 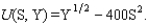 If she chooses S to maximize her expected utility, how much will she study?
If she chooses S to maximize her expected utility, how much will she study?
(Multiple Choice)
4.9/5  (36)
(36)
If someone has strictly convex preferences between all contingent commodity bundles, then he or she must be risk averse.
(True/False)
5.0/5  (38)
(38)
If Paul is risk loving and his basketball team has a probability of .5 of winning, then Paul would rather bet $10 on his team than $100. (When Paul bets X, he wins X if his team wins and loses X if his team loses.)
(True/False)
4.8/5  (40)
(40)
Sally Kink is an expected utility maximizer with utility function pu(c1) + (1 - p)u(c2), where for any x < $3,000, u(x) = 2x, and for x greater than or equal to $3,000, u(x) = 3,0001 + x.
(Multiple Choice)
4.9/5  (36)
(36)
Prufrock is risk averse. He is offered a gamble in which with probability 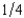 he will lose $1,000 and with probability
he will lose $1,000 and with probability 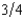 , he will win $500.
, he will win $500.
(Multiple Choice)
4.7/5  (27)
(27)
Diego has $6,400. He plans to bet on a soccer game. Team A is a favorite to win. Assume no ties can occur. For $.80 one can buy a ticket that will pay $1 if team A wins and nothing if B wins. For $.20 one can buy a ticket that pays $1 if team B wins and nothing if A wins. Diego thinks the two teams are equally likely to win. He buys tickets so as to maximize the expected value of lnW (the natural log of his wealth). After he buys his tickets, team A loses a star player and the ticket price moves to $.50 for either team. Diego buys some new tickets and sells some of his old ones. The game is then played and team A wins. How much wealth does he end up with?
(Multiple Choice)
4.9/5  (43)
(43)
Showing 1 - 20 of 39
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)