Exam 12: Simple Regression

In a two-tailed test for correlation at α = .05, a sample correlation coefficient r = 0.42 with n = 25 is significantly different than zero.

Pedro became interested in vehicle fuel efficiency, so he performed a simple regression using 93 cars to estimate the model CityMPG = β₀ + β₁ Weight, where Weight is the weight of the vehicle in pounds. His results are shown below. Write a brief analysis of these results, using what you have learned in this chapter. Is the intercept meaningful in this regression? Make a prediction of CityMPG when Weight = 3000 and also when Weight = 4000. Do these predictions seem believable? If you could make a car 1000 pounds lighter, what change would you predict in its CityMPG? Regression Analysis 0.711 n 93 r-0.843 k1 Std. Error 3.038 Dep. Var. CityMPG $\text { ANOVA table }$ Source SS df MS F p -value Regression 2,065.5191 1 2,065.5191 223.75 2.97-26 Residual 840.0508 91 9.2313 Total 2,905.5699 92 $\text { Rearession outout }$ $\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$ $\text { confidence interval }$ variables coefficients std. error t(df=91) p -value 95\% lower 95\% upper Intercept 47.0484 1.6799 28.006 1.63-46 43.7114 50.3853 Weight -0.0080 0.0005 -14.958 2.97-26 -0.0091 -0.0070

In a sample of n = 23, the Student's t test statistic for a correlation of r = .500 would be:

If R² = .36 in the model Sales = 268 + 7.37 Ads, then Ads explains 36 percent of the variation in Sales.

In a simple bivariate regression with 60 observations, there will be _____ residuals.

When using the least squares method, the column of residuals always sums to zero.

The fitted intercept in a regression has little meaning if no data values near X = 0 have been observed.

Using a two-tailed test at α = .05 for n = 30, we would reject the hypothesis of zero correlation if the absolute value of r exceeds:

Which is not an assumed characteristic of ε_i in the population model y_i = β₀ + β₁ x_i + ε_i?

A variable transformation in a regression (e.g., replacing Y with log(Y)):

Find the slope of the simple regression $\hat { y }$ = b₀ + b₁x. X Y 3 9 5 13 9 10 13 23 15 35

In a simple bivariate regression, F_calc = t_calc².

A scatter plot is used to visualize the association (or lack of association) between two quantitative variables.

The correlation coefficient r always has the same sign as b₁ in Y = b₀ + b₁X.

In least squares regression, the residuals e₁, e₂,…, e_n will always have a zero mean.

Cause-and-effect direction between X and Y may be determined by running the regression twice and seeing whether Y = β₀ + β₁X or X = β₁ + β₀Y has the larger R².

A local trucking company fitted a regression to relate the cost of its shipments as a function of the distance traveled. The Excel fitted regression is shown. 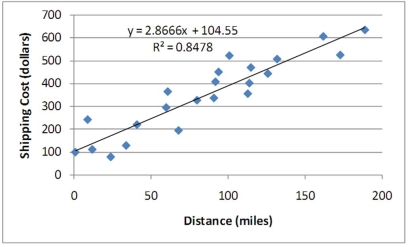Based on this estimated relationship, when distance increases by 50 miles, the expected shipping cost would increase by:

In a simple regression, the F statistic is calculated by taking the ratio of MSR to the MSE.

Pearson's correlation coefficient (r) requires that both variables be interval or ratio data.

In a simple regression, if the coefficient for X is positive and significantly different from zero, then an increase in X is associated with an increase in the mean (i.e., the expected value) of Y.