Exam 11: Bridges to Calculus - an Introduction to Limits
Exam 1: Equations and Inequalities107 Questions
Exam 2: Relations, Functions and Graphs196 Questions
Exam 3: Polynomial and Rational Functions122 Questions
Exam 4: Exponential and Logarithmic Functions96 Questions
Exam 5: Introduction to Trigonometric Functions133 Questions
Exam 6: Trigonometric Identities, Inverses, and Equations97 Questions
Exam 7: Applications of Trigonometry86 Questions
Exam 8: Systems of Equations and Inequalities102 Questions
Exam 9: Analytical Geometry122 Questions
Exam 10: Additional Topics in Algebra121 Questions
Exam 11: Bridges to Calculus - an Introduction to Limits40 Questions
Exam 12: Review of Basic Concepts and Skills112 Questions
Select questions type
Use a table of values to evaluate the function as x approaches the value indicated. If the function seems to approach a limiting value, write the relationship using limit notation. 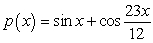 ; x 0
; x 0
Free
(Multiple Choice)
4.9/5  (40)
(40)
Correct Answer:
C
See if a table of values suggests a limit for the function and approach indicated. 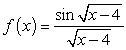 as x 4 from the right
as x 4 from the right
Free
(Multiple Choice)
4.8/5  (34)
(34)
Correct Answer:
B
Use the graphs of f and g to evaluate the limits necessary to complete the calculation. If the computation is not possible, state why. f (x) g (x) 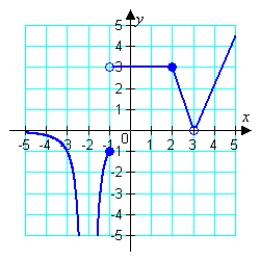
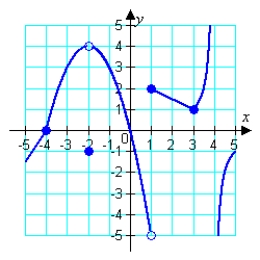
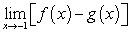
Free
(Multiple Choice)
4.8/5  (42)
(42)
Correct Answer:
A
Evaluate the limits using a table of values. Given 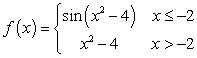 , find:
I.
, find:
I. 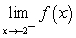 ii.
ii. 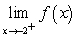
(Multiple Choice)
4.8/5  (34)
(34)
Find the limit of the difference quotient for the function f (x) given, to obtain a function 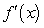 that represents the instantaneous rate of change at x for the function.
that represents the instantaneous rate of change at x for the function. 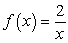
(Multiple Choice)
4.9/5  (41)
(41)
Use a table of values to evaluate the following limit at negative infinity. 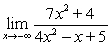
(Multiple Choice)
4.9/5  (28)
(28)
Find the limit of the difference quotient of the given function f (x) to obtain a function 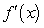 that represents the slope of a line drawn tangent to the curve at x. Use the results to find the slope of the line tangent to the graph of f (x) at x = -3.
that represents the slope of a line drawn tangent to the curve at x. Use the results to find the slope of the line tangent to the graph of f (x) at x = -3. 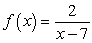
(Multiple Choice)
4.8/5  (39)
(39)
Find the limit of the difference quotient for the function f (x) given, to obtain a function 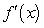 that represents the instantaneous rate of change at x for the function.
that represents the instantaneous rate of change at x for the function. 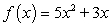
(Multiple Choice)
4.8/5  (37)
(37)
Evaluate the limits using a table of values. Given 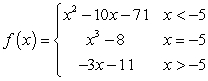 , find:
I.
, find:
I. 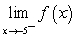 ii.
ii. 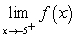 iii.
iii. 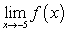
(Multiple Choice)
4.9/5  (26)
(26)
Find the area under the curve for the function and interval given, using the rectangle method and n subintervals of equal width. 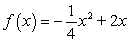 ,
, 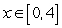
(Multiple Choice)
4.9/5  (36)
(36)
Evaluate the limits using limit properties. If a limit does not exist, state why. 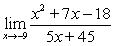
(Multiple Choice)
4.7/5  (33)
(33)
Evaluate the limits using a table of values. Given 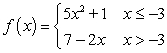 , find:
I.
, find:
I. 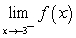 ii.
ii. 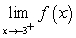 iii.
iii. 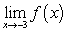
(Multiple Choice)
4.7/5  (39)
(39)
Find the limit of the difference quotient for the function f (x) given, to obtain a function 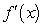 that represents the instantaneous rate of change at x for the function.
that represents the instantaneous rate of change at x for the function. 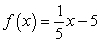
(Multiple Choice)
5.0/5  (32)
(32)
Use a table of values to evaluate the following limit at positive infinity. 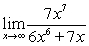
(Multiple Choice)
4.8/5  (35)
(35)
Showing 1 - 20 of 40
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)