Exam 11: Bridges to Calculus - an Introduction to Limits
Exam 1: Equations and Inequalities107 Questions
Exam 2: Relations, Functions and Graphs196 Questions
Exam 3: Polynomial and Rational Functions122 Questions
Exam 4: Exponential and Logarithmic Functions96 Questions
Exam 5: Introduction to Trigonometric Functions133 Questions
Exam 6: Trigonometric Identities, Inverses, and Equations97 Questions
Exam 7: Applications of Trigonometry86 Questions
Exam 8: Systems of Equations and Inequalities102 Questions
Exam 9: Analytical Geometry122 Questions
Exam 10: Additional Topics in Algebra121 Questions
Exam 11: Bridges to Calculus - an Introduction to Limits40 Questions
Exam 12: Review of Basic Concepts and Skills112 Questions
Select questions type
Evaluate the limits using limit properties. If a limit does not exist, state why. 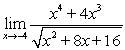
(Multiple Choice)
5.0/5  (41)
(41)
The function g (x) 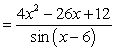 has a hole (discontinuity) in its graph at x = 6. Write a related piecewise-defined function that creates a continuous graph.
has a hole (discontinuity) in its graph at x = 6. Write a related piecewise-defined function that creates a continuous graph.
(Multiple Choice)
4.7/5  (45)
(45)
The population of a small town can be modeled by the function 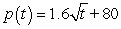 , where p is measured in thousands and t is the number of years after 2008. Find the limit of the difference quotient for p, to obtain a function
, where p is measured in thousands and t is the number of years after 2008. Find the limit of the difference quotient for p, to obtain a function 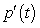 that represents the instantaneous rate of change of population at time t. Use the results to find the instantaneous rate of change of the population of the town in 2024 to the nearest person/yr.
that represents the instantaneous rate of change of population at time t. Use the results to find the instantaneous rate of change of the population of the town in 2024 to the nearest person/yr.
(Multiple Choice)
5.0/5  (35)
(35)
For a new machine shop employee, the rate of production for a specialized part is modeled by the function 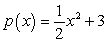 (production increases quickly with experience), where
(production increases quickly with experience), where 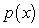 represents the number of parts completed per day. The area under this curve in the interval
represents the number of parts completed per day. The area under this curve in the interval 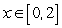 represents the total number of parts produced in the first two days. Using the rectangle method results in the expression
represents the total number of parts produced in the first two days. Using the rectangle method results in the expression 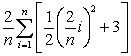 . Find the number of parts produced by applying the summation properties/formulas and taking the limit as n .
. Find the number of parts produced by applying the summation properties/formulas and taking the limit as n .
(Multiple Choice)
4.8/5  (37)
(37)
Evaluate the limits using limit properties. If a limit does not exist, state why. 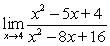
(Multiple Choice)
5.0/5  (34)
(34)
Use a table of values to evaluate the following limit at negative infinity. 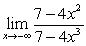
(Multiple Choice)
4.8/5  (34)
(34)
Evaluate the limit by dividing the numerator and denominator by the highest power of x occurring in the denominator. 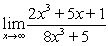
(Multiple Choice)
4.8/5  (38)
(38)
Evaluate the limit by rewriting the given expression as needed. 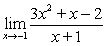
(Multiple Choice)
4.9/5  (36)
(36)
A window washer's bucket falls off a scaffold 248 feet above the street. Its height in feet, t seconds after it falls, can be modeled by 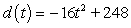 . Find the limit of the difference quotient for d, to obtain a function
. Find the limit of the difference quotient for d, to obtain a function 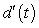 that represents the instantaneous velocity of the bucket at time t. Use the results to find the instantaneous velocity of the bucket at t = 3.
that represents the instantaneous velocity of the bucket at time t. Use the results to find the instantaneous velocity of the bucket at t = 3.
(Multiple Choice)
4.8/5  (39)
(39)
Evaluate the limits using a table of values. Given 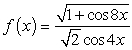 , find:
I.
, find:
I. 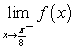 ii.
ii. 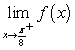 iii.
iii. 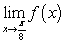
(Multiple Choice)
5.0/5  (47)
(47)
Evaluate the limit by using direct substitution, if possible. If not possible, state why. 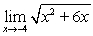
(Multiple Choice)
4.9/5  (31)
(31)
Evaluate the limit by rewriting the given expression as needed. 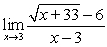
(Multiple Choice)
4.9/5  (37)
(37)
Find the limit of the difference quotient for the function f (x) given, to obtain a function 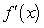 that represents the instantaneous rate of change at x for the function.
that represents the instantaneous rate of change at x for the function. 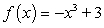
(Multiple Choice)
4.8/5  (44)
(44)
Evaluate the limit by using direct substitution, if possible. If not possible, state why. 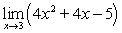
(Multiple Choice)
4.8/5  (39)
(39)
Showing 21 - 40 of 40
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)