Exam 27: Game Theory-Part A

A famous Big Ten football coach had only two strategies, Run the ball to the left side of the line and Run the ball to the right side.The defense can concentrate forces on the left side or the right side.If the opponent concentrates on the wrong side, his offense is sure to gain at least 5 yards.If the defense defended the left side and the offense ran left, the offense gained only 1 yard.If the opponent defended the right side when the offense ran right, the offense would still gain at least 5 yards with probability .70.It is the last play of the game and the famous coach's team is on offense.If it makes 5 yards or more, it wins; if not, it loses.Both sides choose Nash equilibrium strategies.In equilibrium the offense

Suppose that in a Hawk-Dove game similar to the one discussed in your workbook, the payoff to each player is -9 if both play Hawk.If both play Dove, the payoff to each player is 4, and if one plays Hawk and the other plays Dove, the one that plays Hawk gets a payoff of 5 and the one that plays Dove gets 0.In equilibrium, we would expect hawks and doves to do equally well.This happens when the proportion of the total population that plays Hawk is

Big Pig and Little Pig have two possible strategies, Press the Button, and Wait at the Trough.If both pigs choose Wait at the Trough, both get 2.If both pigs choose Press the Button, then Big Pig gets 5 and Little Pig gets 5.If Little Pig presses the button and Big Pig waits at the trough, then Big Pig gets 10 and Little Pig gets 0.Finally, if Big Pig presses the button and Little Pig waits at the trough, then Big Pig gets 6 and Little Pig gets 2.In Nash equilibrium,

While game theory predicts noncooperative behavior for a single play of the prisoner's dilemma, it would predict cooperative tit-for-tat behavior if the same people play prisoner's dilemma together for, say, 20 rounds.

Suppose that in a Hawk-Dove game similar to the one discussed in your workbook, the payoff to each player is -6 if both play Hawk.If both play Dove, the payoff to each player is 4, and if one plays Hawk and the other plays Dove, the one that plays Hawk gets a payoff of 6 and the one that plays Dove gets 0.In equilibrium, we would expect hawks and doves to do equally well.This happens when the proportion of the total population that plays Hawk is

Frank and Nancy met at a sorority sock hop.They agreed to meet for a date at a local bar the next week.Regrettably, they were so fraught with passion that they forgot to agree on which bar would be the site of their rendezvous.Luckily, the town has only two bars, Rizotti's and the Oasis.Having discussed their tastes in bars at the sock hop, both are aware that Frank prefers Rizotti's to the Oasis and Nancy prefer the Oasis to Rizotti's.In fact, the payoffs are as follows.If both go to the Oasis, Nancy's utility is 3 and Frank's utility is 2.If both go to Rizotti's, Frank's utility is 3 and Nancy's utility is 2.If they don't both go to the same bar, both have a utility of 0.

In the town of Torrelodones, each of the N > 2 inhabitants has $100.They are told that they can all voluntarily contribute to a fund that will be evenly divided among all residents.If $F are contributed to the fund, the local K-Mart will match the private contributions so that the total amount to be divided is $2F.That is, each resident will get back a payment of $2F/N when the fund is divided.If the people in town care only about their own net incomes, in Nash equilibrium, how much will each person contribute to the fund?

Two players are engaged in a game of Chicken.There are two possible strategies, Swerve and Drive Straight.A player who chooses to Swerve is called Chicken and gets a payoff of zero, regardless of what the other player does.A player who chooses to Drive Straight gets a payoff of 432 if the other player swerves and a payoff of -48 if the other player also chooses to Drive Straight.This game has two pure strategy equilibria and

Big Pig and Little Pig have two possible strategies, Press the Button, and Wait at the Trough.If both pigs choose Wait at the Trough, both get 3.If both pigs choose Press the Button, then Big Pig gets 8 and Little Pig gets 2.If Little Pig presses the button and Big Pig waits at the trough, then Big Pig gets 10 and Little Pig gets 0.Finally, if Big Pig presses the button and Little Pig waits at the trough, then Big Pig gets 2 and Little Pig gets 1.In Nash equilibrium,

Suppose that in a Hawk-Dove game similar to the one discussed in your workbook, the payoff to each player is -6 if both play Hawk.If both play Dove, the payoff to each player is 3, and if one plays Hawk and the other plays Dove, the one that plays Hawk gets a payoff of 8 and the one that plays Dove gets 0.In equilibrium, we would expect hawks and doves to do equally well.This happens when the proportion of the total population that plays Hawk is

The coach of the offensive football team has two options on the next play.He can run the ball or he can pass.His rival can defend either against the run or against the pass.Suppose that the offense passes.Then if the defense defends against the pass, the offense will make zero yards, and if the defense defends against the run, the offense will make 25 yards.Suppose that the offense runs.If the defense defends against the pass, the offense will make 10 yards, and if the defense defends against a run, the offense will gain 2 yards. a.Write down a payoff matrix for this game. b.Is there a Nash equilibrium in pure strategies for this game? If so, what is it? If not, demonstrate that there is none.

In the game matrix below, the first payoff in each pair goes to player A who chooses the row, and the second payoff goes to player B, who chooses the column.Let a, b, c, and d be positive constants. 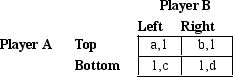If player A chooses Bottom and player B chooses Right in a Nash equilibrium, then we know that

If the number of persons who attend the club meeting this week is X, then the number of people who will attend next week is 63 + 0.30X.What is a long-run equilibrium attendance for this club?

In a Nash equilibrium, everyone must be playing a dominant strategy.

A dominant strategy equilibrium is a set of choices such that each player's choices are optimal regardless of what the other players choose.

A famous Big Ten football coach had only two strategies, Run the ball to the left side of the line and Run the ball to the right side.The defense can concentrate forces on the left side or the right side.If the opponent concentrates on the wrong side, his offense is sure to gain at least 5 yards.If the defense defended the left side and the offense ran left, the offense gained only 1 yard.If the opponent defended the right side when the offense ran right, the offense would still gain at least 5 yards with probability .30.It is the last play of the game and the famous coach's team is on offense.If it makes 5 yards or more, it wins; if not, it loses.Both sides choose Nash equilibrium strategies.In equilibrium the offense

Two players are engaged in a game of Chicken.There are two possible strategies, Swerve and Drive Straight.A player who chooses to Swerve is called Chicken and gets a payoff of zero, regardless of what the other player does.A player who chooses to Drive Straight gets a payoff of 36 if the other player swerves and a payoff of -36 if the other player also chooses to Drive Straight.This game has two pure strategy equilibria and

In Nash equilibrium, each player is making an optimal choice for herself, given the choices of the other players.

George and Sam have taken their fathers' cars out on a lonely road and are engaged in a game of Chicken.George has his father's Mercedes and Sam has his father's rattly little Yugoslavian-built subcompact car.Each of the players can choose either to Swerve or to Not Swerve.If both choose Swerve, both get a payoff of zero.If one chooses Swerve and the other chooses Not Swerve, the one who chooses Not Swerve gets a payoff of 10 and the one who chooses Swerve gets zero.If both choose Not Swerve, the damage to George's car is fairly minor and he gets a payoff of -5, while for Sam the results are disastrous and he gets a payoff of -100.

A famous Big Ten football coach had only two strategies, Run the ball to the left side of the line and Run the ball to the right side.The defense can concentrate forces on the left side or the right side.If the opponent concentrates on the wrong side, his offense is sure to gain at least 5 yards.If the defense defended the left side and the offense ran left, the offense gained only 1 yard.If the opponent defended the right side when the offense ran right, the offense would still gain at least 5 yards with probability .50.It is the last play of the game and the famous coach's team is on offense.If it makes 5 yards or more, it wins; if not, it loses.Both sides choose Nash equilibrium strategies.In equilibrium the offense