Exam 4: Lines parabolas and Systems
Exam 1: Review of Algebra470 Questions
Exam 2: Applications and More Algebra229 Questions
Exam 3: Functions and Graphs237 Questions
Exam 4: Lines parabolas and Systems218 Questions
Exam 5: Exponential and Logarithmic Functions258 Questions
Exam 6: Mathematics of Finance205 Questions
Exam 7: Matrix Algebra173 Questions
Exam 8: Linear Programming44 Questions
Exam 9: Introduction to Probability and Statistics126 Questions
Exam 10: Additional Topics in Probability45 Questions
Exam 11: Limits and Continuity241 Questions
Exam 12: Differentiation283 Questions
Exam 13: Additional Differentiation Topics191 Questions
Exam 14: Curve Sketching161 Questions
Exam 15: Integration261 Questions
Exam 16: Methods and Applications of Integration152 Questions
Exam 17: Continuous Random Variables88 Questions
Exam 18: Multivariable Calculus108 Questions
Select questions type
Two species of monkey,A and B,live in one enclosure at the zoo where they are fed two vitamin supplements.Each day they receive 350 grams of the first supplement and 500 grams of the second supplement.Each monkey of species A requires 25 g of the first supplement and 10 g of the second supplement.Each monkey of species B requires 15 g of the first supplement and 30 g of the second supplement.How many of each species of monkey will the enclosure support so that all of the supplements are consumed each day?
(Short Answer)
4.8/5  (37)
(37)
How much of each of a 25% (by volume)chemical solution and a 32% solution must be combined to make 75 cubic centimeters of a 28% solution?
(Essay)
4.8/5  (32)
(32)
The demand function for a manufacturer's product is p = f(q)= 800 - 2q,where p is the price (in dollars)per unit when q units are demanded (per week).Find the level of production that maximizes the manufacturer's total revenue.
(Multiple Choice)
4.7/5  (32)
(32)
The demand function for an appliance company's line of washing machines is 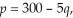 where p is the price (in dollars)per unit when q units are demanded (per week)by consumers.Find the level of production that will maximize the manufacturer's total revenue,and determine this revenue.
where p is the price (in dollars)per unit when q units are demanded (per week)by consumers.Find the level of production that will maximize the manufacturer's total revenue,and determine this revenue.
(Short Answer)
4.9/5  (44)
(44)
Find the Break Even Point for a product whose Total Revenue, 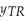 ,(in $)and Total Cost,
,(in $)and Total Cost, 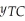 ,(in $)are as follows:
,(in $)are as follows: 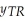 = (10q - 25)q
= (10q - 25)q 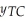 = 2000 + 75q
= 2000 + 75q
(Short Answer)
4.8/5  (36)
(36)
Suppose that a manufacturer will place on the market 80 units of a product when the price is $10 per unit,and 100 units when the price is $12 per unit.Find the supply equation for the product assuming that price p and quantity q are linearly related.
(Multiple Choice)
4.9/5  (40)
(40)
Consider the restricted quadratic function f (x)= 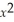 + 4x + 6 on x ≥ -2.Determine the restricted function
+ 4x + 6 on x ≥ -2.Determine the restricted function 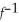 (x)graphically.Graph both f(x)and
(x)graphically.Graph both f(x)and 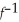 (x)on the same xy-plane.
(x)on the same xy-plane.
(Essay)
4.8/5  (33)
(33)
Solve the following system algebraically: 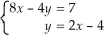
(Not Answered)
This question doesn't have any answer yet
Find the x-coordinate of the vertex of a graph of the quadratic function 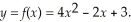
(Multiple Choice)
4.8/5  (44)
(44)
Suppose f is a linear function such that f(0)= 6 and f(3)= 4.Find f(x).
(Essay)
4.9/5  (41)
(41)
Suppose that consumers will demand 800 units of a product when the price is $10 per unit,and 1000 units when the price is $8 per unit.Find the demand equation for the product assuming that price p and quantity q are linearly related.
(Essay)
4.9/5  (35)
(35)
In testing an experimental diet for goats,it was determined that the (average)live weight w (in kilograms)of a goat was statistically a linear function of the number of days d after the diet was started where 0 ≤ d ≤ 100.The weight of a goat starting the diet was 12 kg and 25 days later it was 20 kg.Determine w as a linear function of d and find the average weight of a goat when d = 80.
(Short Answer)
4.7/5  (41)
(41)
Suppose that the supply and demand equations for a certain product are 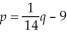 and
and 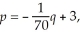 respectively,where p represents the price per unit in dollars and q represents the number of units per time period.
(a)Find the equilibrium price algebraically.
(b)Find the equilibrium price when a tax of 50 cents per unit is imposed.
respectively,where p represents the price per unit in dollars and q represents the number of units per time period.
(a)Find the equilibrium price algebraically.
(b)Find the equilibrium price when a tax of 50 cents per unit is imposed.
(Essay)
4.8/5  (34)
(34)
State whether f(x)= 12 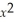 - 24x + 10 has maximum or minimum value and find that value.
- 24x + 10 has maximum or minimum value and find that value.
(Short Answer)
4.9/5  (42)
(42)
Two species of fish,A and B,are raised in one pond at a fish farm where they are fed two vitamin supplements.Each day they receive 100 grams of the first supplement and 200 grams of the second supplement.Each fish of species A requires 20 mg of the first supplement and 30 mg of the second supplement.Each fish of species B requires 10 mg of the first supplement and 40 mg of the second supplement.How many of each species of fish will the pond support so that all of the supplements are consumed each day? Use elimination by substitution to solve the systems.
(Short Answer)
4.8/5  (28)
(28)
Showing 81 - 100 of 218
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)