Exam 14: Curve Sketching
Exam 1: Review of Algebra470 Questions
Exam 2: Applications and More Algebra229 Questions
Exam 3: Functions and Graphs237 Questions
Exam 4: Lines parabolas and Systems218 Questions
Exam 5: Exponential and Logarithmic Functions258 Questions
Exam 6: Mathematics of Finance205 Questions
Exam 7: Matrix Algebra173 Questions
Exam 8: Linear Programming44 Questions
Exam 9: Introduction to Probability and Statistics126 Questions
Exam 10: Additional Topics in Probability45 Questions
Exam 11: Limits and Continuity241 Questions
Exam 12: Differentiation283 Questions
Exam 13: Additional Differentiation Topics191 Questions
Exam 14: Curve Sketching161 Questions
Exam 15: Integration261 Questions
Exam 16: Methods and Applications of Integration152 Questions
Exam 17: Continuous Random Variables88 Questions
Exam 18: Multivariable Calculus108 Questions
Select questions type
Find the absolute extrema for y = 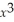 +
+ 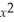 - 3x + 7 on the interval
- 3x + 7 on the interval 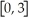 and where they occur.
and where they occur.
(Essay)
4.9/5  (34)
(34)
The demand equation for a monopolist's product is p = 2700 - 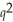 ,where p is the price per unit (in dollars)when q units are demanded.
(a)Find the value of q for which revenue is maximum.
(b)What is the maximum revenue?
,where p is the price per unit (in dollars)when q units are demanded.
(a)Find the value of q for which revenue is maximum.
(b)What is the maximum revenue?
(Essay)
4.8/5  (34)
(34)
A rectangular plot of ground is to be fenced in so that it has an area of 15,000 square feet.The plot is to be divided in half with a fence parallel to one pair of sides.Find the dimensions of the plot if the least amount of fencing is to be used.
(Short Answer)
4.8/5  (32)
(32)
If y = 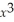 + 4
+ 4 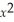 - 3x + 4,use the second-derivative test to find all values of x for which (a)relative maxima occur (b)relative minima occur.
- 3x + 4,use the second-derivative test to find all values of x for which (a)relative maxima occur (b)relative minima occur.
(Essay)
4.8/5  (40)
(40)
The revenue equation for a company is given by R(x)= 68.04x - 0.07 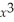 .Determine when relative extrema occur on the interval (0,∞).
.Determine when relative extrema occur on the interval (0,∞).
(Short Answer)
4.8/5  (43)
(43)
Sensitivity to a drug depends on the dosage size x according to the equation s = 100x - 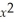 .Find the dosage that maximizes sensitivity.
.Find the dosage that maximizes sensitivity.
(Short Answer)
4.9/5  (36)
(36)
An open box is to be made by cutting equal squares from each corner of a 20-in.square piece of cardboard and then folding up the sides.Find the length of the side of the square that must be cut out if the volume of the box is to be maximized.
(Essay)
4.8/5  (39)
(39)
Let y = 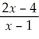 (a)Determine all x - and y-intercepts.
(b)Determine equations of all vertical asymptotes and non-vertical asymptotes.
(c)Determine y' and y''.
(d)Determine intervals on which the function is increasing; determine intervals on which the function is decreasing.
(e)Determine the coordinates of all relative maximum and relative minimum points.
(f)Determine intervals on which the function is concave up; determine intervals on which the function is concave down.
(g)Determine the coordinates of all inflection points.
(h)With the aid of the information obtained in parts (a)- (g),give a reasonable sketch of the curve.
(a)Determine all x - and y-intercepts.
(b)Determine equations of all vertical asymptotes and non-vertical asymptotes.
(c)Determine y' and y''.
(d)Determine intervals on which the function is increasing; determine intervals on which the function is decreasing.
(e)Determine the coordinates of all relative maximum and relative minimum points.
(f)Determine intervals on which the function is concave up; determine intervals on which the function is concave down.
(g)Determine the coordinates of all inflection points.
(h)With the aid of the information obtained in parts (a)- (g),give a reasonable sketch of the curve.
(Essay)
4.9/5  (41)
(41)
The graph of a function is given.Find
(a)the open intervals on which the function is increasing or decreasing;
(b)the coordinates of all relative extrema. 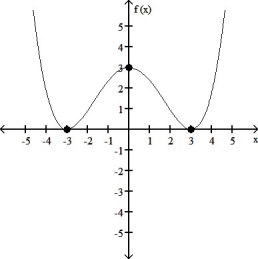
(Essay)
4.8/5  (36)
(36)
Find two numbers whose sum is 50 and such that the product of one of them and five more than the other is a maximum.
(Essay)
4.8/5  (29)
(29)
On the interval 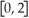 ,the function y =
,the function y = 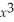 + 3
+ 3 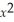 - 9x + 27 has an absolute maximum when x =
- 9x + 27 has an absolute maximum when x =
(Multiple Choice)
4.7/5  (28)
(28)
The profit equation for a taco stand is given by P(x)= -0.4 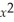 + 100x - 100,where x is the number of tacos sold,and P(x)is the profit in dollars.Use the first-derivative test to find when relative extrema occur.
+ 100x - 100,where x is the number of tacos sold,and P(x)is the profit in dollars.Use the first-derivative test to find when relative extrema occur.
(Essay)
4.8/5  (39)
(39)
The cost equation for a cookie store is given by C(x)= 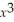 - 6
- 6 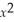 + 250,where x is the number of cookies made (in dozens)and C(x)is the cost in dollars.Use the first-derivative test to find when relative extrema occur.
+ 250,where x is the number of cookies made (in dozens)and C(x)is the cost in dollars.Use the first-derivative test to find when relative extrema occur.
(Essay)
4.8/5  (37)
(37)
Let y = 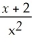 (a)Determine all x - and y-intercepts.
(b)Determine equations of all vertical asymptotes and non-vertical asymptotes.
(c)Determine y' and y''.
(d)Determine intervals on which the function is increasing; determine intervals on which the function is decreasing.
(e)Determine the coordinates of all relative maximum and relative minimum points.
(f)Determine intervals on which the function is concave up; determine intervals on which the function is concave down.
(g)Determine the coordinates of all inflection points.
(h)With the aid of the information obtained in parts (a)- (g),give a reasonable sketch of the curve.
(a)Determine all x - and y-intercepts.
(b)Determine equations of all vertical asymptotes and non-vertical asymptotes.
(c)Determine y' and y''.
(d)Determine intervals on which the function is increasing; determine intervals on which the function is decreasing.
(e)Determine the coordinates of all relative maximum and relative minimum points.
(f)Determine intervals on which the function is concave up; determine intervals on which the function is concave down.
(g)Determine the coordinates of all inflection points.
(h)With the aid of the information obtained in parts (a)- (g),give a reasonable sketch of the curve.
(Essay)
4.8/5  (44)
(44)
Use the second derivative test to find the relative extremas of f(x)= 4 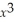 - 6x and where they occur.If the relative extremas can not be determined by the second derivative test,state so.
- 6x and where they occur.If the relative extremas can not be determined by the second derivative test,state so.
(Essay)
4.7/5  (38)
(38)
Showing 41 - 60 of 161
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)