Exam 18: Multivariable Calculus
Exam 1: Review of Algebra470 Questions
Exam 2: Applications and More Algebra229 Questions
Exam 3: Functions and Graphs237 Questions
Exam 4: Lines parabolas and Systems218 Questions
Exam 5: Exponential and Logarithmic Functions258 Questions
Exam 6: Mathematics of Finance205 Questions
Exam 7: Matrix Algebra173 Questions
Exam 8: Linear Programming44 Questions
Exam 9: Introduction to Probability and Statistics126 Questions
Exam 10: Additional Topics in Probability45 Questions
Exam 11: Limits and Continuity241 Questions
Exam 12: Differentiation283 Questions
Exam 13: Additional Differentiation Topics191 Questions
Exam 14: Curve Sketching161 Questions
Exam 15: Integration261 Questions
Exam 16: Methods and Applications of Integration152 Questions
Exam 17: Continuous Random Variables88 Questions
Exam 18: Multivariable Calculus108 Questions
Select questions type
Use the method of Lagrange multipliers to determine the critical points of f(x,y)= 4 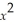 + 2
+ 2 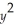 + 3 subject to the constraint x+ 2y = 9.
+ 3 subject to the constraint x+ 2y = 9.
(Short Answer)
4.8/5  (43)
(43)
The production function for a company's product is P = 100L + 50k - 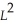 -
- 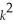 ,where P is the output that results from L units of labor and k units of capital.The unit costs of labor and capital are 6 and 3,respectively.If the company wants the total cost of inputs to be 30,determine the greatest output possible subject to this budget constraint.
,where P is the output that results from L units of labor and k units of capital.The unit costs of labor and capital are 6 and 3,respectively.If the company wants the total cost of inputs to be 30,determine the greatest output possible subject to this budget constraint.
(Short Answer)
4.8/5  (33)
(33)
An empirical formula relating the surface area A (in square inches)of an average human body to the weight (in pounds)and the height h (in inches)of the person is A(w,h)= 15.64 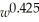
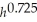 .Find
.Find 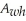 and
and 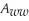 .
.
(Essay)
4.9/5  (32)
(32)
A manufacturer produces products A and B for which the average costs of production are constant at 3 and 5 (dollars per unit),respectively.The quantities 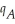 ,
, 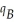 of A and B that can be sold each week are given by the joint-demand functions
of A and B that can be sold each week are given by the joint-demand functions 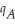 = 10 -
= 10 - 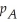 +
+ 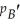 and
and 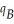 = 12 +
= 12 + 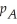 - 3
- 3 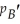 where
where 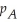 and
and 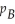 are the prices (in dollars per unit)of A and B,respectively.Determine the prices of A and B at which the manufacturer can maximize profit.
are the prices (in dollars per unit)of A and B,respectively.Determine the prices of A and B at which the manufacturer can maximize profit.
(Essay)
4.8/5  (40)
(40)
A sporting goods store determines that the optimal quantity of athletic shoes (in pairs)to order each month is given by the Wilson lot size formula: Q(C,M,s)= 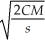 ,where C is the cost (in dollars)of placing an order,M is the number of pairs sold each month,and s is the monthly storage cost (in dollars)per pair of shoes.Find
,where C is the cost (in dollars)of placing an order,M is the number of pairs sold each month,and s is the monthly storage cost (in dollars)per pair of shoes.Find 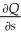 .Then find and interpret
.Then find and interpret 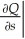
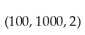 .
.
(Essay)
4.9/5  (36)
(36)
A company manufactures two products,X and Y,and the joint-cost function for these products is given by 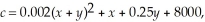 where c is the total cost of producing x units of X and y units of Y.Determine the marginal cost with respect to x when x = 450 and y = 550.
where c is the total cost of producing x units of X and y units of Y.Determine the marginal cost with respect to x when x = 450 and y = 550.
(Short Answer)
4.9/5  (42)
(42)
A sporting goods store determines that the optimal quantity of athletic shoes (in pairs)to order each month is given by the Wilson lot size formula: Q(C,M,s)= 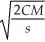 ,where C is the cost (in dollars)of placing an order,M is the number of pairs sold each month,and s is the monthly storage cost (in dollars)per pair of shoes.Find
,where C is the cost (in dollars)of placing an order,M is the number of pairs sold each month,and s is the monthly storage cost (in dollars)per pair of shoes.Find 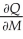 .Then find and interpret
.Then find and interpret 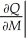
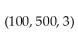 .
.
(Essay)
4.9/5  (38)
(38)
The Cobb-Douglas production function for a company is given by P(k,l)= 163 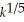
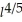 where P is the monthly production value when k is the number of units of capital and l is the number of units of labor.Suppose that capital costs $105 per unit,labor costs $70 per unit,and the total cost of capital and labor is limited to $152,250.Use Lagrange Multipliers to write the system of equations you would use to find the number of units of capital and labor that maximize production.
where P is the monthly production value when k is the number of units of capital and l is the number of units of labor.Suppose that capital costs $105 per unit,labor costs $70 per unit,and the total cost of capital and labor is limited to $152,250.Use Lagrange Multipliers to write the system of equations you would use to find the number of units of capital and labor that maximize production.
(Essay)
4.8/5  (40)
(40)
A television manufacturing company makes two types of TV's.The cost of producing x units of type A and y units of type B is given by the function C(x,y)= 100 + 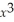 + 64
+ 64 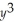 - 96xy.How many units of type A and type B televisions should the company produce to minimize its cost?
- 96xy.How many units of type A and type B televisions should the company produce to minimize its cost?
(Short Answer)
4.9/5  (42)
(42)
The Cobb-Douglas production function for a company is given by P(k,l)= 70 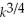
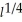 where P is the monthly production value when k is the number of units of capital and l is the number of units of labor.Suppose that capital costs $450 per unit,labor costs $75 per unit,and the total cost of capital and labor is limited to $60,000.Use Lagrange multipliers to write the system of equations you would use to find the number of units of capital and labor that maximize production.
where P is the monthly production value when k is the number of units of capital and l is the number of units of labor.Suppose that capital costs $450 per unit,labor costs $75 per unit,and the total cost of capital and labor is limited to $60,000.Use Lagrange multipliers to write the system of equations you would use to find the number of units of capital and labor that maximize production.
(Essay)
4.8/5  (40)
(40)
For the production function P = 5.4 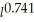
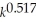 ,find the marginal productivity functions
,find the marginal productivity functions 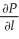 and
and 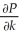 .
.
(Essay)
4.8/5  (45)
(45)
A sporting goods store determines that the optimal quantity of athletic shoes (in pairs)to order each month is given by the Wilson lot size formula: Q(C,M,s)= 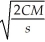 ,where C is the cost (in dollars)of placing an order,M is the number of pairs sold each month,and s is the monthly storage cost (in dollars)per pair of shoes.Find
,where C is the cost (in dollars)of placing an order,M is the number of pairs sold each month,and s is the monthly storage cost (in dollars)per pair of shoes.Find 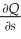 .Then find and interpret
.Then find and interpret 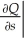
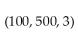 .
.
(Essay)
4.7/5  (36)
(36)
Determine the critical points of f(x,y)= 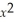 + xy +
+ xy + 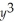 - y and also determine by the second-derivative test whether each point corresponds to a relative maximum,to a relative minimum,to neither,or whether the test gives no information.
- y and also determine by the second-derivative test whether each point corresponds to a relative maximum,to a relative minimum,to neither,or whether the test gives no information.
(Essay)
4.7/5  (42)
(42)
Showing 21 - 40 of 108
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)