Exam 11: Comparisons Involving Proportions and a Test of Independence

The sampling distribution of 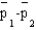is approximated by a

The degrees of freedom for a contingency table with 6 rows and 3 columns is

Exhibit 11-4 In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College. -Refer to Exhibit 11-4. The hypothesis is to be tested at the 5% level of significance. The critical value from the table equals

A goodness of fit test is always conducted as a

Exhibit 11-7 The results of a recent poll on the preference of shoppers regarding two products are shown below. 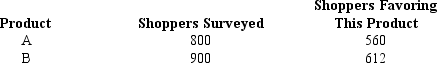-Refer to Exhibit 11-7. The 95% confidence interval estimate for the difference between the populations favoring the products is

Before the start of the Winter Olympics, it was expected that the percentages of medals awarded to the top contenders to be as follows. Midway through the Olympics, of the 120 medals awarded, the following distribution was observed. We want to test to see if there is a significant difference between the expected and actual awards given. a.Compute the test statistic. b.Using the p-value approach, test to see if there is a significant difference between the expected and the actual values. Let $\alpha$ = .05. c.At 95% confidence, test for a significant difference using the critical value approach.

Exhibit 11-7 The results of a recent poll on the preference of shoppers regarding two products are shown below. 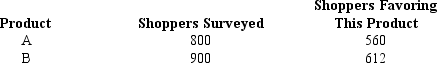-Refer to Exhibit 11-7. The point estimate for the difference between the two population proportions in favor of this product is

Exhibit 11-4 In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College. -Refer to Exhibit 11-4. The calculated value for the test statistic equals

Exhibit 11-3 In order to determine whether or not a particular medication was effective in curing the common cold, one group of patients was given the medication, while another group received sugar pills. The results of the study are shown below. 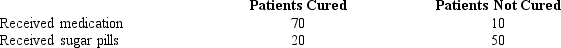We are interested in determining whether or not the medication was effective in curing the common cold. -Refer to Exhibit 11-3. The p-value is

Exhibit 11-2 Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification. We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year. -Refer to Exhibit 11-2. At 95% confidence, the null hypothesis

Exhibit 11-9 The results of a recent poll on the preference of teenagers regarding the types of music they listen to are shown below. 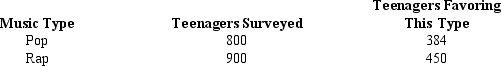-Refer to Exhibit 11-9. The point estimate for the difference between the proportions is

The results of a recent poll on the preference of voters regarding presidential candidates are shown below. At 95% confidence, test to determine whether or not there is a significant difference between the preferences for the two candidates.

Exhibit 11-8 An insurance company selected samples of clients under 18 years of age and over 18 and recorded the number of accidents they had in the previous year. The results are shown below. We are interested in determining if the accident proportions differ between the two age groups. -Refer to Exhibit 11-8. The pooled proportion is

Exhibit 11-2 Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification. We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year. -Refer to Exhibit 11-2. The expected frequency of seniors is

Five hundred randomly selected automobile owners were questioned on the main reason they had purchased their current automobile. The results are given below. 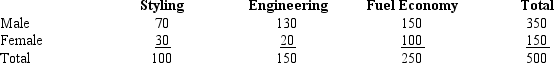a.State the null and alternative hypotheses for a contingency table test. b.State the decision rule for the critical value approach. Let $\alpha$ = .01. c.Calculate the $\chi$ ² test statistic. d.Give your conclusion for this test.

The makers of Compute-All know that in the past, 40% of their sales were from people under 30 years old, 45% of their sales were from people who are between 30 and 50 years old, and 15% of their sales were from people who are over 50 years old. A sample of 300 customers was taken to see if the market shares had changed. In the sample, 100 of the people were under 30 years old, 150 people were between 30 and 50 years old, and 50 people were over 50 years old. a.State the null and alternative hypotheses to be tested. b.Compute the test statistic. c.The null hypothesis is to be tested at the 1% level of significance. Determine the critical value from the table. d.What do you conclude?

Exhibit 11-2 Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification. We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year. -Refer to Exhibit 11-2. The p-value is

In the last presidential election, before the candidates started their major campaigns, the percentages of registered voters who favored the various candidates were as follows. After the major campaigns began, a random sample of 400 voters showed that 172 favored the Republican candidate; 164 were in favor of the Democratic candidate; and 64 favored the Independent candidate. We are interested in determining whether the proportion of voters who favored the various candidates had changed. a.Compute the test statistic. b.Using the p-value approach, test to see if the proportions have changed. c.Using the critical value approach, test the hypotheses.

Exhibit 11-5 The table below gives beverage preferences for random samples of teens and adults. We are asked to test for independence between age (i.e., adult and teen) and drink preferences. -Refer to Exhibit 11-5. With a .05 level of significance, the critical value for the test is

Last school year, in the school of Business Administration, 30% were Accounting majors, 24% Management majors, 26% Marketing majors, and 20% Economics majors. A sample of 300 students taken from this year's students of the school showed the following number of students in each major: 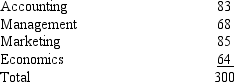We want to see if there has been a significant change in the number of students in each major. a.Compute the test statistic. b.Has there been any significant change in the number of students in each major between the last school year and this school year. Use the p-value approach and let $\alpha$ = .05.