Exam 6: Continuous Probability Distributions

The First National Mortgage Company has noted that 6% of its customers pay their mortgage payments after the due date. a.What is the probability that in a random sample of 150 customers 7 will be late on their payments? b.What is the probability that in a random sample of 150 customers at least 10 will be late on their payments?

Which of the following is not a characteristic of the normal probability distribution?

Exhibit 6-1 The assembly time for a product is uniformly distributed between 6 to 10 minutes. -Refer to Exhibit 6-1. The expected assembly time (in minutes) is

Exhibit 6-7 The weight of items produced by a machine is normally distributed with a mean of 8 ounces and a standard deviation of 2 ounces. -Refer to Exhibit 6-7. What is the probability that a randomly selected item will weigh between 11 and 12 ounces?

Exhibit 6-5 The travel time for a college student traveling between her home and her college is uniformly distributed between 40 and 90 minutes. -Refer to Exhibit 6-5. The probability that her trip will take exactly 50 minutes is

Exhibit 6-7 The weight of items produced by a machine is normally distributed with a mean of 8 ounces and a standard deviation of 2 ounces. -Refer to Exhibit 6-7. What percentage of items will weigh between 6.4 and 8.9 ounces?

A normal distribution with a mean of 0 and a standard deviation of 1 is called

Exhibit 6-8 The life expectancy of a particular brand of tire is normally distributed with a mean of 40,000 and a standard deviation of 5,000 miles. -Refer to Exhibit 6-8. What percentage of tires will have a life of 34,000 to 46,000 miles?

Exhibit 6-4 f(x) =(1/10) e^-x/10 x 0 -Refer to Exhibit 6-4. The mean of x is

Approximate the following binomial probabilities by the use of normal approximation. a.P(x < 12, n = 50, p = 0.3) b.P(12 < x < 18, n = 50, p = 0.3)

Given that Z is a standard normal random variable. What is the value of Z if the area to the left of Z is 0.9382?

Consider a binomial probability experiment with n = 3 and p = 0.1. Then, the probability of x = 0 is

The price of a stock is uniformly distributed between $30 and $40. a.What is the probability that the stock price will be more than $37? b.What is the probability that the stock price will be less than or equal to $32? c.What is the probability that the stock price will be between $34 and $38? d.Determine the expected price of the stock. e. Determine the standard deviation for the stock price.

Exhibit 6-7 The weight of items produced by a machine is normally distributed with a mean of 8 ounces and a standard deviation of 2 ounces. -Refer to Exhibit 6-7. What percentage of items will weigh at least 11.7 ounces?

Z is a standard normal random variable. The P (1.41 < Z < 2.85) equals

A professor at a local community college noted that the grades of his students were normally distributed with a mean of 74 and a standard deviation of 10. The professor has informed us that 6.3 percent of his students received A's while only 2.5 percent of his students failed the course and received F's. a.What is the minimum score needed to make an A? b.What is the maximum score among those who received an F? c.If there were 5 students who did not pass the course, how many students took the course?

Z is a standard normal random variable. The P(-1.96 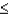Z 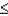-1.4) equals

A continuous random variable may assume

For a continuous random variable x, the probability density function f(x) represents

Given that Z is a standard normal random variable, what is the probability that Z -2.12?