Exam 5: Systems of Equations and Inequalities
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 1: Equations and Inequalities94 Questions
Exam 2: Functions and Graphs97 Questions
Exam 3: Polynomial and Rational Functions105 Questions
Exam 4: Exponential and Logarithmic Functions92 Questions
Exam 5: Systems of Equations and Inequalities94 Questions
Exam 6: Matrices and Determinants94 Questions
Exam 7: Sequences, Series, and Probability92 Questions
Select questions type
Use a graphing utility to find the point(s) of intersection of the graphs. 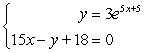
(Multiple Choice)
4.8/5  (43)
(43)
Sketch the graph of the solution set of each system of inequalities. 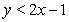
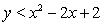
(Multiple Choice)
4.9/5  (37)
(37)
Use the statements below to write a system of equations.Solve the system by elimination. The sum of twice a number  and a number
and a number 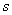 is -14.The difference of
is -14.The difference of 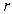 and
and 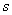 is 2.
is 2.
(Multiple Choice)
4.8/5  (41)
(41)
One acetic acid solution is 60% water and another is 40% water.How many liters of each solution should be mixed to produce 20 liters of a solution that is 49% water?
(Multiple Choice)
4.7/5  (34)
(34)
You invest $3700 in a fishing lure business.A lure costs $1.60 to produce and will be sold for $6.20.How many lures must you sell to break even?
(Multiple Choice)
4.7/5  (38)
(38)
An accounting firm charges $2500 for an audit and $350 for a tax return.Research and available resources have indicated the following constraints. The firm has 900 hours of staff time available each week.
The firm has 155 hours of review time available each week.
Each audit requires 75 hours of staff time and 10 hours of review time.
Each tax return requires 12.5 hours of staff time and 2.5 hours of review time.
The accounting firm lowers its charge for an audit to $2000.What numbers of audits and tax returns will bring in an optimal revenue?
(Multiple Choice)
4.9/5  (42)
(42)
A manufacturer produces two models of bicycles.The times (in hours) required for assembling, painting, and packaging each model are shown in the table. Process  The total times available for assembling, painting, and packing are 4000 hours, 4800 hours, and 1500 hours, respectively.The profit per unit are $50 for model A and $75 for model B.What is the optimal production level for each model? What is the optimal profit?
The total times available for assembling, painting, and packing are 4000 hours, 4800 hours, and 1500 hours, respectively.The profit per unit are $50 for model A and $75 for model B.What is the optimal production level for each model? What is the optimal profit?
(Multiple Choice)
4.8/5  (42)
(42)
Graph the solution set of the system of inequalities below. 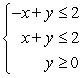
(Multiple Choice)
4.9/5  (41)
(41)
Which of the following vertices of the constraint region shown is a minimum value of the objective function below. 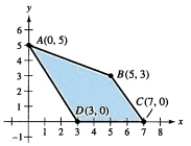
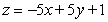
(Multiple Choice)
4.9/5  (48)
(48)
Find an equation of the form 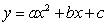 whose graph passes through the points
whose graph passes through the points 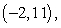
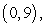 and
and 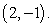
(Multiple Choice)
4.9/5  (33)
(33)
Use back-substitution to solve the system of linear equations. 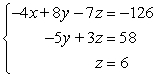
(Multiple Choice)
4.8/5  (31)
(31)
A farming cooperative mixes two brands of cattle feed.Brand X costs $30 per bag, and brand Y costs $25 per bag.Research and available resources have indicated the following constraints. Brand X contains two units nutritional element A, two units of element B, and two units of element C.
Brand Y contains one unit of nutritional element A, nine units of element B, and three units of element C.
The minimum requirements for nutrients A, B, and C are 12 units, 36 units, and 24 units, respectively.
What is the optimal number of bags of each brand that should be mixed? What is optimal cost?
(Multiple Choice)
4.9/5  (35)
(35)
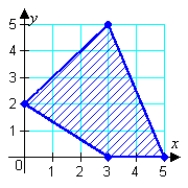
Find the minimum and maximum values of the objective function and where they occur, subject to the indicated constraints. Objective function: 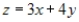 Constraints:
Constraints: 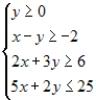
(Multiple Choice)
4.9/5  (39)
(39)
Find the consumer surplus for the pair of demand and supply equations below. 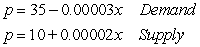
(Multiple Choice)
4.7/5  (38)
(38)
Determine which one of the ordered triples below is a solution of the given system of equations. 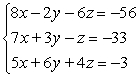
(Multiple Choice)
4.9/5  (34)
(34)
For the given supply and demand equations, find the consumer surplus. Round to the nearest dollar. Demand Supply
P = 170 - 0.00003x p = 140 + 0.00004x
(Multiple Choice)
4.8/5  (43)
(43)
Showing 41 - 60 of 94
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)