Exam 7: Extension G: Differential Equations
Exam 1: Extension A: Functions and Models20 Questions
Exam 1: Extension B: Functions and Models5 Questions
Exam 1: Extension C: Functions and Models8 Questions
Exam 1: Extension D: Functions and Models12 Questions
Exam 1: Extension E: Functions and Models7 Questions
Exam 1: Extension F: Functions and Models5 Questions
Exam 2: Extension A: Limits and Derivatives9 Questions
Exam 2: Extension B: Limits and Derivatives5 Questions
Exam 2: Extension C: Limits and Derivatives6 Questions
Exam 2: Extension D: Limits and Derivatives6 Questions
Exam 2: Extension E : Limits and Derivatives5 Questions
Exam 2: Extension F: Limits and Derivatives5 Questions
Exam 2: Extension G: Limits and Derivatives10 Questions
Exam 2: Extension H: Limits and Derivatives5 Questions
Exam 3: Extension A: Differentiation Rules5 Questions
Exam 3: Extension B: Differentiation Rules11 Questions
Exam 3: Extension C: Differentiation Rules8 Questions
Exam 3: Extension D: Differentiation Rules5 Questions
Exam 3: Extension E: Differentiation Rules4 Questions
Exam 3: Extension F: Differentiation Rules5 Questions
Exam 3: Extension G: Differentiation Rules5 Questions
Exam 4: Extension A: Applications of Differentiation17 Questions
Exam 4: Extension B: Applications of Differentiation8 Questions
Exam 4: Extension C: Applications of Differentiation15 Questions
Exam 4: Extension D: Applications of Differentiation5 Questions
Exam 4: Extension E: Applications of Differentiation12 Questions
Exam 4: Extension F: Applications of Differentiation5 Questions
Exam 4: Extension G: Applications of Differentiation12 Questions
Exam 5: Extension A: Integrals5 Questions
Exam 5: Extension B: Integrals10 Questions
Exam 5: Extension C: Integrals7 Questions
Exam 5: Extension D: Integrals5 Questions
Exam 5: Extension E: Integrals7 Questions
Exam 6: Extension A: Applications of Integration9 Questions
Exam 6: Extension B: Applications of Integration14 Questions
Exam 6: Extension C: Applications of Integration7 Questions
Exam 6: Extension D: Applications of Integration5 Questions
Exam 6: Extension E: Applications of Integration5 Questions
Exam 6: Extension F: Applications of Integration6 Questions
Exam 7: Extension A: Differential Equations11 Questions
Exam 7: Extension B: Differential Equations13 Questions
Exam 7: Extension C: Differential Equations5 Questions
Exam 7: Extension D: Differential Equations8 Questions
Exam 7: Extension E: Differential Equations7 Questions
Exam 7: Extension F: Differential Equations16 Questions
Exam 7: Extension G: Differential Equations10 Questions
Exam 8: Extension A: Infinte Sequences and Series6 Questions
Exam 8: Extension B: Infinte Sequences and Series11 Questions
Exam 8: Extension C: Infinte Sequences and Series7 Questions
Exam 8: Extension D: Infinte Sequences and Series5 Questions
Exam 8: Extension E: Infinte Sequences and Series6 Questions
Exam 8: Extension F: Infinte Sequences and Series5 Questions
Exam 8: Extension G: Infinte Sequences and Series8 Questions
Exam 8: Extension H: Infinte Sequences and Series5 Questions
Exam 9: Extension A: Vectors and the Geometry of Space5 Questions
Exam 9: Extension B: Vectors and the Geometry of Space5 Questions
Exam 9: Extension C: Vectors and the Geometry of Space5 Questions
Exam 9: Extension D: Vectors and the Geometry of Space6 Questions
Exam 9: Extension E: Vectors and the Geometry of Space9 Questions
Exam 10: Extension A: Vector Functions9 Questions
Exam 10: Extension B: Vector Functions5 Questions
Exam 10: Extension C: Vector Functions5 Questions
Exam 10: Extension D: Vector Functions7 Questions
Exam 10: Extension E: Vector Functions10 Questions
Exam 10: Extension F: Vector Functions4 Questions
Exam 10: Extension H: Vector Functions5 Questions
Exam 10: Extension G: Vector Functions9 Questions
Exam 10: Extension H: Vector Functions14 Questions
Exam 11: Extension A: Partial Derivatives5 Questions
Exam 11: Extension B: Partial Derivatives13 Questions
Exam 11: Extension C: Partial Derivatives17 Questions
Exam 11: Extension D: Partial Derivatives8 Questions
Exam 11: Extension E: Partial Derivatives5 Questions
Exam 11: Extension F: Partial Derivatives5 Questions
Exam 11: Extension G: Partial Derivatives14 Questions
Exam 11: Extension H: Partial Derivatives6 Questions
Exam 12: Extension A: Multiple Integrals5 Questions
Exam 12: Extension B: Multiple Integrals10 Questions
Exam 12: Extension C: Multiple Integrals11 Questions
Exam 12: Extension D: Multiple Integrals5 Questions
Exam 12: Extension E: Multiple Integrals11 Questions
Exam 12: Extension F: Multiple Integrals5 Questions
Exam 12: Extension G: Multiple Integrals6 Questions
Exam 12: Extension H: Multiple Integrals6 Questions
Exam 13: Extension A: Vector Calculus5 Questions
Exam 13: Extension B: Vector Calculus7 Questions
Exam 13: Extension C: Vector Calculus5 Questions
Exam 13: Extension D: Vector Calculus6 Questions
Exam 13: Extension E: Vector Calculus10 Questions
Exam 13: Extension F: Vector Calculus5 Questions
Exam 13: Extension G: Vector Calculus5 Questions
Exam 13: Extension H: Vector Calculus9 Questions
Exam 13: Extension I: Vector Calculus3 Questions
Select questions type
Choose the differential equation corresponding to this direction field. 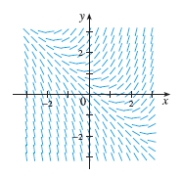
Free
(Multiple Choice)
4.9/5  (28)
(28)
Correct Answer:
B
Find the solution of the differential equation 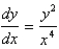 that satisfies the initial condition
that satisfies the initial condition 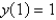
Free
(Essay)
4.8/5  (31)
(31)
Correct Answer:
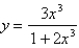
Biologists stocked a lake with 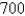 fish and estimated the carrying capacity (the maximal population for the fish of that species in that lake)to be
fish and estimated the carrying capacity (the maximal population for the fish of that species in that lake)to be 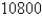 The number of fish tripled in the first year.Assuming that the size of the fish population satisfies the logistic equation,find an expression for the size of the population after t years.
The number of fish tripled in the first year.Assuming that the size of the fish population satisfies the logistic equation,find an expression for the size of the population after t years.
Free
(Essay)
4.8/5  (30)
(30)
Correct Answer:
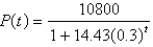
A tank contains 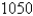 L of brine with
L of brine with 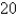 kg of dissolved salt.Pure water enters the tank at a rate of
kg of dissolved salt.Pure water enters the tank at a rate of 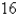 L/min.The solution is kept thoroughly mixed and drains from the tank at the same rate.How much salt is in the tank after
L/min.The solution is kept thoroughly mixed and drains from the tank at the same rate.How much salt is in the tank after 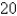 minutes?
minutes?
(Essay)
4.7/5  (35)
(35)
One model for the spread of an epidemic is that the rate of spread is jointly proportional to the number of infected people and the number of uninfected people.In an isolated town of 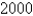 inhabitants,
inhabitants, 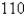 people have a disease at the beginning of the week and
people have a disease at the beginning of the week and 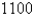 have it at the end of the week.How long does it take for
have it at the end of the week.How long does it take for 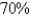 of the population to be infected?
of the population to be infected?
(Multiple Choice)
4.9/5  (40)
(40)
A certain small country has $20 billion in paper currency in circulation,and each day $70 million comes into the country's banks.The government decides to introduce new currency by having the banks replace old bills with new ones whenever old currency comes into the banks.Let 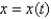 denote the amount of new currency in circulation at time t with
denote the amount of new currency in circulation at time t with 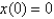 Formulate and solve a mathematical model in the form of an initial-value problem that represents the "flow" of the new currency into circulation (in billions per day).
Formulate and solve a mathematical model in the form of an initial-value problem that represents the "flow" of the new currency into circulation (in billions per day).
(Essay)
4.8/5  (31)
(31)
The Pacific halibut fishery has been modeled by the differential equation 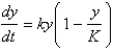 where
where 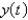 is the biomass (the total mass of the members of the population)in kilograms at time t (measured in years),the carrying capacity is estimated to be
is the biomass (the total mass of the members of the population)in kilograms at time t (measured in years),the carrying capacity is estimated to be 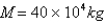 and
and 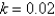 per year.If
per year.If 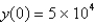 ,find the biomass a year later.
,find the biomass a year later.
(Essay)
4.8/5  (33)
(33)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)