Exam 9: Basic Oligopoly Models
Exam 1: The Fundamentals of Managerial Economics143 Questions
Exam 2: Market Forces: Demand and Supply150 Questions
Exam 3: Quantitative Demand Analysis170 Questions
Exam 4: The Theory of Individual Behavior179 Questions
Exam 5: The Production Process and Costs173 Questions
Exam 6: The Organization of the Firm157 Questions
Exam 7: The Nature of Industry123 Questions
Exam 8: Managing in Competitive, Monopolistic, and Monopolistically Competitive Markets130 Questions
Exam 9: Basic Oligopoly Models134 Questions
Exam 10: Game Theory: Inside Oligopoly140 Questions
Exam 11: Pricing Strategies for Firms With Market Power140 Questions
Exam 12: The Economics of Information128 Questions
Exam 13: Advanced Topics in Business Strategy89 Questions
Exam 14: A Managers Guide to Government in the Marketplace112 Questions
Select questions type
Two identical firms compete as a Cournot duopoly. The demand they face is P = 100 - 2Q. The cost function for each firm is C(Q) = 4Q. In equilibrium, the deadweight loss is:
(Multiple Choice)
4.9/5  (38)
(38)
Two identical firms compete as a Cournot duopoly. The demand they face is P = 100 - 2Q. The cost function for each firm is C(Q) = 4Q. Each firm earns equilibrium profits of:
(Multiple Choice)
4.7/5  (42)
(42)
With linear demand and constant marginal cost, a Stackelberg leader's profits are ___________ the follower.
(Multiple Choice)
4.8/5  (39)
(39)
Two firms compete in a Stackelberg fashion. If firm 2 is the leader, then:
(Multiple Choice)
5.0/5  (37)
(37)
A new firm enters a market which is initially serviced by a Cournot duopoly charging a price of $10. What will the new market price be should the three firms coexist after the entry?
(Multiple Choice)
4.9/5  (37)
(37)
Which of the following is NOT a quantity-setting oligopoly model?
(Multiple Choice)
4.8/5  (41)
(41)
The (inverse) demand in a Cournot duopoly is P = a - b (Q1 + Q2), and costs are C1(Q1) = c1Q1 and C2(Q2) = c2Q2. Show that the Cournot equilibrium levels of output are 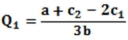 and
and 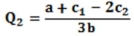 .
.
(Essay)
4.8/5  (33)
(33)
Both firms in a Cournot duopoly would enjoy higher profits if:
(Multiple Choice)
4.8/5  (33)
(33)
Consider two firms competing to sell a homogeneous product by setting price. The inverse demand curve is given by P = 6 - Q. If each firm's cost function is Ci(Qi) = 2Qi, then consumer surplus in this market is:
(Multiple Choice)
4.7/5  (29)
(29)
Consider a market consisting of two firms where the inverse demand curve is given by P = 500 - 2Q1 - 2Q2. Each firm has a marginal cost of $50. Based on this information, we can conclude that consumer surplus in the different equilibrium oligopoly models will follow which of the following orderings?
(Multiple Choice)
4.9/5  (44)
(44)
Consider a Stackelberg duopoly with the following inverse demand function: P = 100 - 2Q1 - 2Q2. The firms' marginal costs are identical and are given by MCi(Qi) = ciQi. Based on this information, the Stackelberg leader's marginal revenue function is:
(Multiple Choice)
4.9/5  (38)
(38)
Which of the following is a profit-maximizing condition for a Cournot oligopolist?
(Multiple Choice)
4.8/5  (46)
(46)
Consider a Stackelberg duopoly with the following inverse demand function: P = 100 - 2Q1 - 2Q2. The firms' marginal costs are identical and are given by MCi(Qi) = 2. Based on this information, the leader's reaction function is:
(Multiple Choice)
4.7/5  (41)
(41)
Which of the following is true about a differentiated-product Bertrand duopoly?
(Multiple Choice)
4.9/5  (47)
(47)
Showing 81 - 100 of 134
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)