Exam 14: Chi-Square Applications
Exam 1: What Is Statistics79 Questions
Exam 2: Describing Data: Frequency Tables, Frequency Distributions, and Graphic Presentation87 Questions
Exam 3: Describing Data: Numerical Measures191 Questions
Exam 4: A Survey of Probability Concepts130 Questions
Exam 5: Discrete Probability Distributions121 Questions
Exam 6: Continuous Probability Distributions143 Questions
Exam 7: Sampling Methods and the Central Limit Theorem78 Questions
Exam 8: Estimation and Confidence Intervals134 Questions
Exam 9: One-Sample Tests of Hypothesis139 Questions
Exam 10: Two-Sample Tests of Hypothesis103 Questions
Exam 11: Analysis of Variance97 Questions
Exam 12: Linear Regression and Correlation166 Questions
Exam 13: Multiple Regression and Correlation Analysis128 Questions
Exam 14: Chi-Square Applications126 Questions
Exam 15: Index Numbers93 Questions
Exam 16: Time Series and Forecasting90 Questions
Exam 17: An Introduction to Decision Theory54 Questions
Select questions type
How many degrees of freedom do we use for the chi square goodness of fit test?
(Multiple Choice)
4.8/5  (44)
(44)
Three new colors have been proposed for the Jeep Grand Cherokee vehicle. They are silvered-blue, almond, and willow green. The null hypothesis for a goodness-of-fit test would be
(Multiple Choice)
4.8/5  (39)
(39)
A student asked a statistics professor if grades were marked "on the curve." The professor decided to give the student a project to determine if last year's statistics grades were normally distributed. The professor told the student that last year's mean mark was 70 with a standard deviation of 10 and to use the following results. 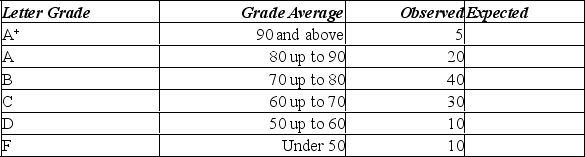
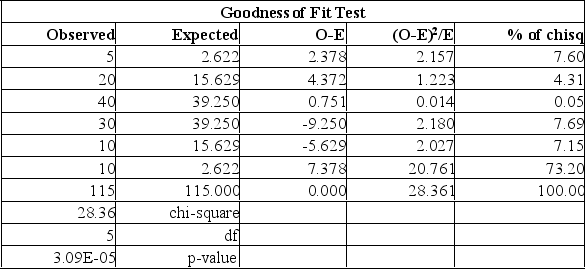 Using the data from this Mega stat printout, you determine:
Using the data from this Mega stat printout, you determine:
(Multiple Choice)
4.9/5  (40)
(40)
i. The minimum computed value of chi-square is one. ii. The chi-square distribution is a positively skewed distribution.
iii. The lowest level of data for which the chi-square goodness-of-fit test is appropriate is the nominal level.
(Multiple Choice)
5.0/5  (38)
(38)
At a recent automobile show, a sample of 125 people produced the following results. Use the 0.05 significance level to determine if there is a relationship between age and model preferred. 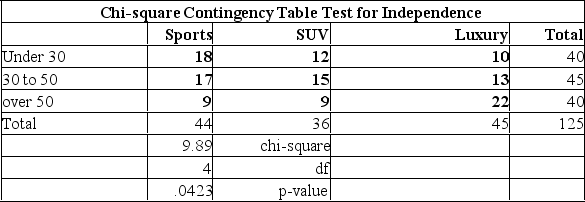 Based on the analysis above, what can be concluded?
Based on the analysis above, what can be concluded?
(Multiple Choice)
4.7/5  (42)
(42)
i. For a goodness-of-fit test, the following are possible null and alternate hypotheses. Null: Sales are uniformly distributed among the five locations. Alternate: Sales are not uniformly distributed among the five locations. ii. In the goodness-of-fit test, the chi-square distribution is used to determine how well an observed set of observations "fits" an "expected" set of observations.
iii. The sum of the expected frequencies and the sum of the observed frequencies must be equal.
(Multiple Choice)
4.9/5  (37)
(37)
What is our decision for a goodness-of-fit test with a computed value of chi-square of 1.273 and a critical value of 13.388?
(Multiple Choice)
4.8/5  (43)
(43)
i. The claim that "male and female University of Toledo students prefer different parking lots on campus" is an example of a chi-square null hypothesis. ii. For contingency table analysis using the chi-square test, multiplying the number of rows minus 1 by the number of columns minus 1 will give you the degrees of freedom.
iii. For a contingency table, the expected frequency for a cell is found by dividing the row total by the grand total.
(Multiple Choice)
4.9/5  (32)
(32)
i. The shape of the chi-square distribution depends on the size of the sample. ii. Small differences between observed and expected frequencies are due to chance.
iii. The chi-square distribution with large degrees of freedom approaches a normal distribution.
(Multiple Choice)
5.0/5  (43)
(43)
At a recent car show, a sample of 125 people produced the following results. Use the 0.01 significance level to determine if there is a relationship between age and model preferred. 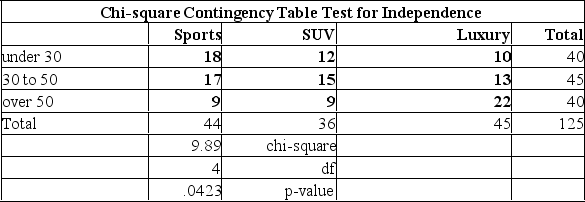
(Multiple Choice)
4.8/5  (44)
(44)
Canadian Accounting classifies accounts receivable as "current", "late", and "not collectible". Industry figures show that 60% of A/R are current, 30% are late, and 10% are uncollectible. A law firm in Markham Ontario has 500 accounts receivable: 320 are current, 100 are late and 80 are not collectible. Are these numbers in agreement with the industry distribution? 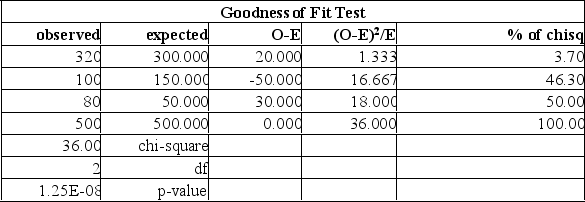 Using the data from this Mega stat printout, you determine:
Using the data from this Mega stat printout, you determine:
(Multiple Choice)
4.8/5  (51)
(51)
The personnel manager is concerned about absenteeism. She decides to sample the records to determine if absenteeism is distributed evenly throughout the six-day workweek. The null hypothesis to be tested is: Absenteeism is distributed evenly throughout the week. The 0.01 level is to be used. The sample results are: 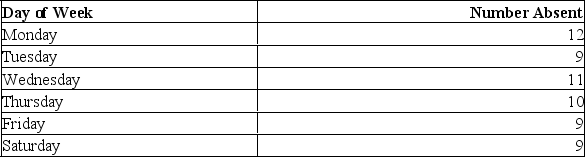 What is the calculated value of chi-square?
What is the calculated value of chi-square?
(Multiple Choice)
4.8/5  (25)
(25)
i. The claim that "male and female University of Toledo students prefer different parking lots on campus" is an example of a chi-square null hypothesis. ii. For a contingency table, the expected frequency for a cell is found by dividing the row total by the grand total.
iii. For contingency table analysis using the chi-square test, multiplying the number of rows minus 1 by the number of columns minus 1 will give you the degrees of freedom.
(Multiple Choice)
4.8/5  (49)
(49)
A survey of the opinions of property owners about a street widening project was taken to determine whether the resulting opinion was related to the distance of front footage. A randomly selected sample of 100 property owners was contacted and the results are shown below.  What is the critical value at the 10% level of significance?
What is the critical value at the 10% level of significance?
(Multiple Choice)
4.8/5  (30)
(30)
i. Nonparametric tests require no assumptions about the shape of the population distribution. ii. There is not one, but a family of chi-square distributions. There is a chi-square distribution for 1 degree of freedom, another for 2 degrees of freedom, another for 3 degrees of freedom, and so on.
iii. The chi-square distribution with large degrees of freedom approaches a normal distribution.
(Multiple Choice)
4.9/5  (28)
(28)
At a recent automobile show, a sample of 125 people produced the following results. Use the 0.01 significance level to determine if there is a relationship between age and model preferred. 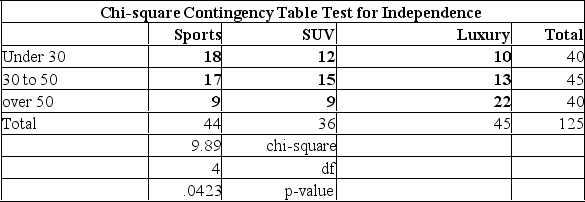 Based on the analysis above, what can be concluded?
Based on the analysis above, what can be concluded?
(Multiple Choice)
4.9/5  (42)
(42)
The following table shows the adjustment to civilian life and place of residence. 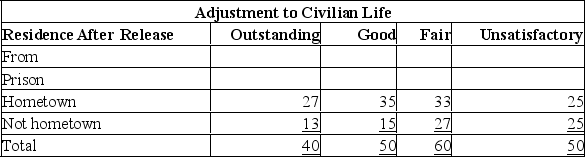 What is the critical value for this contingency table at the 0.01 level of significance?
What is the critical value for this contingency table at the 0.01 level of significance?
(Multiple Choice)
4.7/5  (24)
(24)
i. There is not one, but a family of chi-square distributions. There is a chi-square distribution for 1 degree of freedom, another for 2 degrees of freedom, another for 3 degrees of freedom, and so on. ii. The shape of the chi-square distribution depends on the size of the sample.
iii. Small differences between observed and expected frequencies are due to chance.
(Multiple Choice)
4.8/5  (40)
(40)
Which of the following is not a characteristic of the chi square distribution?
(Multiple Choice)
4.9/5  (40)
(40)
Canadian Accounting classifies accounts receivable as "current", "late", and "not collectible". Industry figures show that 60% of A/R are current, 30% are late, and 10% are uncollectible. A law firm in Markham Ontario has 500 accounts receivable: 310 are current, 125 are late and 65 are not collectible. Are these numbers in agreement with the industry distribution? 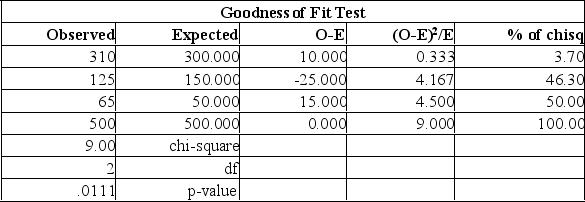 Using the data from this Mega stat printout, you determine:
Using the data from this Mega stat printout, you determine:
(Multiple Choice)
4.8/5  (31)
(31)
Showing 61 - 80 of 126
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)