Exam 8: Estimation and Confidence Intervals

A bank wishes to estimate the mean balances owed by customers holding MasterCard. The population standard deviation is estimated to be $300. If a 98 percent confidence interval is used and an interval of $75 is desired, how many cardholders should be sampled?

The following summarizes the amount of snowfall in Ontario over the past number of years. If 90% and 95% confidence intervals were developed to estimate the true average annual snowfall, what similarities would they have?

When using Student's t to compute an interval estimate,

(i. The interval estimate states the range within which a population parameter probably lies. (ii). The measure of confidence that one has in the interval estimate is called degree of level of confidence. (iii) For a sampling distribution of the means, 90% percent of the means would be between $\pm$ 1.96 standard deviations.

College X is concerned about their employees making use of their email for non-business purposes. You have been approached to assist in this matter. College X decides on a 95% confidence level and state that the estimation proportion must be within 2 percent of the population proportion. A pilot survey reveals that 10 out of 50 emails sampled were not for business purposes. How many emails should be surveyed to meet your requirements?

In order to construct a 90% confidence interval for the population mean when the population standard deviation is unknown and the sample size is 18, you should use the t-value indicated as:

College X is concerned about their employees making use of their email for non-business purposes. You have been approached to assist in this matter. College X decides on a 99% confidence level and state that the estimation proportion must be within 2 percent of the population proportion. A pilot survey reveals that 10 out of 50 emails sampled were not for business purposes. How many emails should be surveyed to meet your requirements?

Mileage tests were conducted on a randomly selected sample of 100 newly developed automobile tires. The average tread life was found to be 80,000 kilometres with a standard deviation of 5,600 kilometres. What is the best estimate of the average tread life in miles for the entire population of these tires?

The Sugar Producers Association wants to estimate the mean yearly sugar consumption. A sample of 16 people reveals the mean yearly consumption to be 27 kg with a sample standard deviation of 9 kg. Assume a normal population. For a 95% confidence interval, what is the critical value needed?

College X is concerned about their employees making use of their email for non-business purposes. A random sample of 400 e-mails discovered 60 messages that were not business related. The 99% confidence interval for the population proportion is:

i. The t distribution is based on the assumption that the population of interest is normal or nearly normal. ii. The t distribution is a discrete distribution. iii. There is not one t distribution, but rather a "family" of t distributions.

A survey of 144 retail stores revealed that the average price of a DVD was $375 with a standard error of $20. What is the 99% confidence interval to estimate the true cost of the DVD?

A group of statistics students decided to conduct a survey at their university to find the average (mean) amount of time students spent studying per week. Assuming a standard deviation of 3 hours, what is the required sample size if the error is to be less than ½ hour with a 99% level of confidence?

The z-value associated with a 94% level of confidence is:

A student wanted to quickly construct a 99% confidence interval for the average age of students in her statistics class. She randomly selected 9 students. Their average age was 19.1 years with a standard deviation of 1.5 years. What is the 99% confidence interval for the population mean?

i. The test statistic t has n-1 degrees of freedom. ii. All t distributions have the same mean of zero and a standard deviation of 1. iii. The t distribution is more spread out and flatter at the center than is the standard normal distribution. However, as the sample size increases, the t distribution curve approaches the standard normal distribution.

The Sugar Producers Association wants to estimate the mean yearly sugar consumption. A sample of 25 people reveals the mean yearly consumption to be 27 kg with a sample standard deviation of 9 kg. Assume a normal population. For a 90% confidence interval, what is the critical value needed?

A statistics professor wishes to estimate the average mark on a term test for a course that has multiple sections and many students. A survey of some of the students registered for the course reveals the following results: 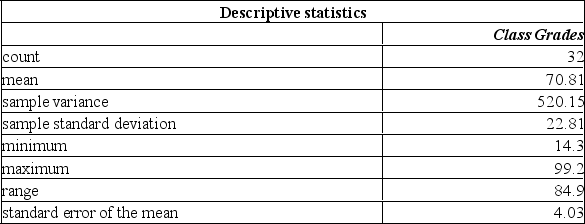The student from the course wonders whether the population mean could have been 60 or 80.

College X is concerned about their employees making use of their email for non-business purposes. A random sample of 400 e-mails discovered 80 messages that were not business related. The 95% confidence interval for the population proportion is:

The distribution of Student's t has